Number Play Class 6 Solutions Questions and Answers
3.1 Numbers can Tell us Things 3.2 Supercells Figure it Out (Page No. 57-58)
Question 1.
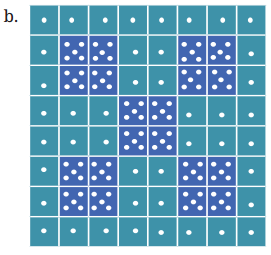
Colour or mark the supercells in the table below.
Solution:
Question 2.
Fill the table below with only 4-digit numbers such that the supercells are exactly the coloured cells.
Solution:
To fill the table with only 4-digit numbers such that the supercells are exactly the coloured cells, we may use many variations of 4-digit numbers, of which one is given below:
We need to keep in mind that a supercell is a cell that contains a number that is larger than its adjacent cells.
Question 3.
Fill the table below such that we get as many supercells as possible. Use numbers between 100 and 1000 without repetitions.
Solution:

Question 4.
Out of the 9 numbers, how many supercells are there in the table above? _____________
Solution:
There are 5 supercells in the above table out of the 9 numbers.
Question 5.
For this group of 5 children, is the sequence 1, 1, 1, 1, 1 possible?
Solution:
No, this sequence is not possible. If every child says ‘1’, it means each child has exactly one taller child adjacent to them. This situation cannot occur with 5 children of different heights as there must be at least one child who is the tallest and another who is the shortest.
Question 6.
Can you fill a supercell table without repeating numbers such that there are no supercells? Why or why not?
Solution:
No, it is not possible to fill a supercell table without repeating numbers such that there are no supercells.
As there are two cases:
Case I: If we fill the cells in descending order then the first cell be supercell.
Case II: If we fill the cells in ascending order then the last cell will be supercell.
If we don’t follow any order, then there will definitely atleast one supercell.
Question 7.
Will the cell having the largest number in a table always be a supercell? Can the cell having the smallest number in a table be a supercell? Why or why not?
Solution:
Yes, the cell having the largest number in a table will always be a supercell, because largest number will always be largest among the other numbers.
But, the cell having smallest number in a table be never be a supercell, because it will always be smallest.
Question 8.
Fill a table such that the cell having the second largest number is not a supercell.
Solution:
Here 980 is the second largest number but it is not a supercell as 999 is the supercell.
Question 9.
Fill a table such that the cell having the second largest number is not a supercell but the second smallest number is a super cell. Is it possible?
Solution:
Here 1870 is the second largest number but the cell having 1870 is not a supercell because number 1895 (adjacent to it) is greater than it.
489 is the second smallest number but the cell having 489 is a supercell because adjacent number 475 is smaller to it.
Question 10.
Make other variations of this puzzle and challenge your classmates.
Solution:
To be done by students on their own.
InText Questions (Pages 58-59)
Question 1.
Complete Table 2 with 5-digit numbers whose digits are ‘1’, ‘0’, ‘6’. ‘3’, and ‘9’ in some order. Only a coloured cell should have a number greater than all its neighbours. (Page 58)
Solution:
| 96,310 | 96,301 | 36,109 | 63,109 |
| 10,369 | 13,609 | 60,319 | 19,306 |
| 10,936 | 36,910 | 60,193 | 39,106 |
| 10,369 | 10,963 | 10,639 | 39,610 |
The biggest number in the table is 96, 310.
The smallest even number in the table is 10,936.
The smallest number greater than 50,000 in the table is 60,193.

3.3 Patterns of Numbers on the Number Line Figure it Out (Page No. 59)
Question 1.
Identify the numbers marked on the number lines below, and label the remaining positions.
Put a circle around the smallest number and a box around the largest number in each of the sequences above.
Solution:
Solution:
Solution:
Solution:
Intext Questions (Page 60)
Question 1.
Find out how many numbers have two digits, three digits, four digits, and five digits:
Solution:
3.4 Playing with Digits (Page No. 60)
Question 1.
Digit sum 14
(a) Write other numbers whose digits add up to 14.
(b) What is the smallest number whose digit sum is 14?
(c) What is the largest 5-digit whose digit sum is 14?
(d) How big a number can you form with the digit sum 14? Can you make an even bigger number?
Solution:
(a) The other numbers whose digits add up to 14 are 374, 473, 284, 482, 824, 842, 248, 428, 347, 437, 743, 734 etc.
(b) 59
(c) 95000
(d)
| Number | Digit Sum |
| 40 | 4 + 0 = 4 |
| 41 | 4 + 1 = 5 |
| 42 | 4 + 2 = 6 |
| 43 | 4 + 3 = 7 |
| 44 | 4 + 4 = 8 |
| 45 | 4 + 5 = 9 |
| 46 | 4 + 6 = 10 |
| 47 | 4 + 7 = 11 |
| 48 | 4 + 8 = 12 |
| 49 | 4 + 9 = 13 |
| 50 | 5 + 0 = 5 |
| 51 | 5 + 1 = 6 |
| 52 | 5 + 2 = 7 |
| 53 | 5 + 3 = 8 |
| 54 | 5 + 4 = 9 |
| 55 | 5 + 5 = 10 |
| 56 | 5 + 6 = 11 |
| 57 | 5 + 7 = 12 |
| 58 | 5 + 8 = 13 |
| 59 | 5 + 9 = 14 |
| 60 | 6 + 0 = 6 |
| 61 | 6 + 1 = 7 |
| 62 | 6 + 2 = 8 |
| 63 | 6 + 3 = 9 |
| 64 | 6 + 4 = 10 |
| 65 | 6 + 5 = 11 |
| 66 | 6 + 6 = 12 |
| 67 | 6 + 7 = 13 |
| 68 | 6 + 8 = 14 |
| 69 | 6 + 9 = 15 |
| 70 | 7 + 0 = 7 |
Question 2.
Find out the digit sums of all the numbers from 40 to 70. Share your observations with the class.
Solution:
Digit sum of 40 = (4 + 0 = 4)
Digit sum of 41 = (4 +1 = 5)
Digit sum of 42 = (4 + 2 = 6)
Digit sum of 43 = (4 + 3 = 7)
Digit sum of 44 = (4 + 4 = 8)
Digit sum of 45 = (4 + 5 = 9)
Digit sum ,of 46 = (4 + 6 = 10)
Digit sum of 47 = (4 + 7 = 11)
Digit sum of 48 = (4 + 8 = 12)
Digit sum of 49 = (4 +9 = 13)
Digit sum of 50 = (5 + 0 = 5)
Digit sum of 51 = (5 + 1 = 6)
Digit sum of 52 = (5 + 2 = 7)
Digit sum of 53 = (5 + 3 = 8)
Digit sum of 54 = (5 + 4 = 9)
Digit sum of 55 = (5 + 5 = 10)
Digit sum of 56 = (5 + 6 = 11)
Digit sum of 57 = (5 + 7 = 12)
Digit sum of 58 = (5 + 8 = 13)
Digit sum of 59 = (5 + 9 = 14)
Digit sum of 60 = (6 + 0 = 6)
Digit sum of 61 = (6 + 1 = 7)
Digit sum of 62 = (6 + 2 = 8)
Digit sum of 63 = (6 + 3 = 9)
Digit sum of 64 = (6 + 4 = 10)
Digit sum of 65 = (6 + 5 = 11)
Digit sum of 66 = (6 + 6 = 12)
Digit sum of 67 = (6 + 7 = 13)
Digit sum of 68 = (6 + 8 = 14)
Digit sum of 69 = (6 + 9 = 15)
Digit sum of 70 = (7 + 0 = 7)
Observations
For numbers 40 to 49, we get
a sequence 4, 5, 6, 7, 8 … 13
For numbers 50 to 59, we get
a sequence 5,6, 7, 8,… 14
For numbers 60 to 69, we get
a sequence 6, 7, 8, 9, 10,,… 15
Here, the sum of the digits of all the numbers from 40 to 70 is present in the numbers from 4 to 15.

Question 3.
Calculate the digit sums of 3-digit numbers whose digits are consecutive (for example, 345). Do you see a pattern? Will this pattern continue?
Solution:
If we take numbers in reverse order, sum of digits will remain same.
Yes, we observe a pattern.
i. e. (first number + 1) × 3 = digit sum.
InText Questions (Page 61)
Question 1.
Among the numbers 1-100, how many times will the digit ‘7’ occur? Among the numbers 1-1000, how many times will the digit ‘7’ occur?
Solution:
There are 10 numbers with 7 in the ones digit, i.e., 7, 17, 27, 37, 47, 57, 67, 77, 87, 97.
There are 10 numbers with 7 in the tens digit, i.e., 70, 71, 72, 73, 74, 75, 76, 77, 78, 79.
So, among the numbers 1-100, digit ‘7’ occur 20 times.
Similarly, from 101-200, 20 times digit ‘7’ occur.
201-300, 20 times digit ‘7’ occur.
301-400, 20 times digit ‘7’ occur.
401-500, 20 times digit ‘7’ occur.
501-600, 20 times digit ‘7’ occur.
601-700, 21 times digit ‘7’ occur.
801-900, 20 times digit ‘7’ occur.
901-1000, 20 times digit ‘7’ occur.
Now, from 701-800,
At hundred place of these 3 digit numbers, 7 will come 100 times.
At tens place 7 will come 10 times, i.e., 770, 771, 772, 773, 774, 775, 775, 777, 778, 779.
At units place 7 will come 10 times, i.e., 707, 717, 727, 737, 747, 757, 767, 777, 787, 797.
So, total number of times digit ‘7’ occurs from 701 – 800 = 100 + 10 + 10 = 120
By adding all, we get 20 × 8 + 120 + 21 = 301
Question 2.
Write all possible 3-digit palindromes using these digits.
Solution:
The possible 3-digit palindromes using the digit 1, 2, 3 are:
111, 121, 212, 131, 222, 232, 313, 323, 333.
InText Questions (Page 62)
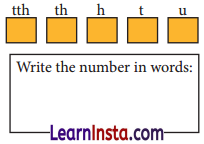
Question 1.
Puzzle time
I am a 5-digit palindrome.
I am an odd number.
My ‘t’ digit is double of my ‘u’ digit.
My ‘h’ digit is double of my ‘t’ digit.
Who am I? _______
Solution:
The required 5-digit od d palindrome number is 12421, where ‘t’ digit is double of ‘u’ digit and ‘h’ digit is double of‘t’ digit.
In words: Twelve thousand four hundred twenty-one.
InText Questions (Page 64)
On the usual 12-hour clock, there are timings with different patterns. For example, 4:44, 10:10, 12:21.
Question 1.
Try and find out all possible times on a 12-hour clock of each of these types.
Solution:
Possible times on a 12-hour clock are as follows: 1:11, 2:22, 11:11, 4:44, 01:01, 12:21 and so on.
Manish has his birthday on 20/12/2012, where the digits ‘2’, ‘0’, ‘ 1 ’ and ‘2’ repeat in that order.
Question 2.
Find some other dates of this form from the past.
Solution:
Possible dates of the form 20/12/2012, where the digits ‘2’, ‘0’, ‘ 1 ’, and ‘2’ repeat in that order are as follows: 12/01/1201, 19/10/1910, 20/11/2011 and so on.
His sister Meghana has her birthday on 11/02/2011 where the digits read the same from left to right and from right to, left.

Question 3.
Find all possible dates of this form from the past.
Solution:
Possible dates of the form 11/02/2011, where the digits read the same from left to right and from right to left are as follows:
10/02/2001, 09/01/1090, 08/02/2080
Jeevan was looking at this year’s calendar. He started wondering, “Why should we change the calendar every year!
Can we not reuse a calendar?” What do you think?
You might have noticed that last year’s calendar was different from this year’s. Also, next year’s calendar is also different from the previous years.
Question 4.
But, will any year’s calendar repeat again after some years? Will all dates and days in a year match exactly with that of another year?
Solution:
Calendar repetition can happen after 6 or 11 years, depending on the leap year. Leap years have 366 days, so these calendars are the same every 28 years.
For example, the 2024 calendar will repeat in 2052, and the 2022 calendar will repeat in 2033.
Yes, all dates and days in a year match exactly with that of another year.
3.5 Pretty Palindromic Patterns 3.6 The Magic Number of Kaprekar 3.7 Clock and Calendar Numbers Figure it Out (Page No. 64-65)
Question 1.
Pratibha uses the digits ‘4‘7’, ‘3’and ‘2’ and makes the smallest and largest 4-digit numbers with them: 2347 and 7432. The difference between these two numbers is 7432 – 2347 = 5085. The sum of these two numbers is 9779. Choose 4-digits to make:
(a) the difference between the largest and smallest numbers greater than 508$.
(b) the difference between the largest and smallest numbers less than 5085.
(e) the sum of the largest and smallest numbers greater than 9779.
(d) the sum of the largest and smallest numbers less than 9779.
Solution:
(a) Digits – 8, 7, 3 and 2
Largest Number – 8 7 3 2
Smallest Number – 2 3 7 8
Difference = 6 3 5 4
6354 > 5085
(b) Digits – 1, 2, 3 and 4
Largest Number – 4 3 2 1
Smallest Number – 1 2 3 4
Difference = 3 0 8 7
3087 < 5085
(c) Digits – 9, 8, 7 and 6
Largest Number – 9 8 7 6
Smallest Number – 6 7 8 9
Sum = 166 6 5
16665 > 9779
(d) Digits – 1, 2, 3 and 8
Largest Number 8 3 2 1
Smallest Number 1 2 3 8
Sum = 9 5 5 9
9559 < 9779
Question 2.
What is the sum of the smallest and largest 5-digit palindrome? What is their difference?
Solution:
Smallest 5-digit palindrome = 10001
Largest 5-digit palindrome = 99999
Sum = 10001+99999 =110000
Difference = 99999 -10001 = 89998
Question 3.
The time now is 10:01. How many minutes until the clock shows the next palindromic time? What about the one after that?
Solution:
Next palindromic time after 10:01 is 11:11 after 70 minutes. After that next palindromic time will be 12:21.

Question 4.
How many rounds does the number 5683 take to reach the Kaprekar constant?
Solution:
The Kaprekar constant for a 4-digit number is 6174. To reach this constant, we apply a process known as Kaprekar’s routine:
- Arrange the digits of the number in descending order.
- Arrange the digits in ascending order.
- Subtract the smaller number from the larger one.
- Repeat the process until the result is 6174.
Let’s apply this to 5683 and see how many rounds it takes to reach the Kaprekar constant.
First round:
- The largest number from digits 5683: 8653
- The smallest number from digits 5683: 3568
- Subtraction: 8653 – 3568 = 5085
Second round:
- Largest number from digits of 5085: 8550
- The smallest number from digits 5085: 0558 (which is 558 when leading zeros are omitted)
- Subtraction: 8550 – 0558 = 7992
Third round:
- The largest number from digits 7992: 9972
- The smallest number from digits 7992: 2799
- Subtraction: 9972 – 2799 = 7173
Fourth round:
- The largest number from digits 7173: 7731
- The smallest number from digits 7173: 1377
- Subtraction: 7731 – 1377 = 6354
Fifth round:
- The largest number from digits 6354: 6543
- The smallest number from digits 6354: 3456
- Subtraction: 6543 – 3456 = 3087
Sixth round:
- The largest number from digits 3087: 8730
- The smallest number from digits 3087: 0378 (or 378)
- Subtraction: 8730 – 0378 = 8352
Seventh round:
- The largest number from digits 8352: 8532
- The smallest number from digits 8352: 2358
- Subtraction: 8532 – 2358 = 6174
Conclusion:
It takes 7 rounds for the number 5683 to reach the Kaprekar constant 6174.
InText Questions (Page 66)
Question 1.
Can we make 1,000 using the numbers in the middle? Why not? What about 14,000, 15,000 and 16,000? Yes, it is possible. Explore how. What thousands cannot be made? (Refer the figure on page 65 of NCERT Textbook)
Solution:
Yes, we can make 1000 using the numbers in the middle.
1000= 1500 – 400 – 400 – 4
14000 = 13000 + 400 × 2 + 400 = 2
15000 = 13000 + 400 × 4 + 400
16000= 13000 + 1500 × 2
3.8 Mental Math Figure it Out (Page No. 66 – 67)
Question 1.
Write an example for each of the below scenarios whenever possible.
Could you find examples for all the cases? If not, think and discuss what could be the reason. Make other such questions and challenge your classmates.
(a) Let’s divide
90, 250 by 2
then
90,2502 = 45,125
Hence to get sum more than 90,250 both numbers should be more than 45,125.
(b) To get a 6 digit sum by adding 5 digit and 3 digit, the 5 digit number should be more than 99,001.
(c) Let’s take minimum 4 digit number 1000
let’s add them
which is a 4 digit number.
Hence 6 digit sum’ from 4 digit number is impossible.
(d) Let’s take 5 digit numbers 67987 and 65783
let’s add them
which is a 6 digit number.
(e) Let’s take minimum 5 digit numbers 1000
let’s add them
which is a 5 digit number.
Hence 6 digit sum from 5 digit numbers is impossible.

(f) 5-digit -5
digit to
give a difference less than 56,503
< 56503
(g) 5-digit-3 digit = 1 008 6 (5 digit)
to give a 4 digit = + 875 (3 digit)
difference = 92 11 (4 digit)
(h) 5-digit digit = 1 2 8 7 6 (5 digit)
to give a 4 digit = -7865 (4 digit)
difference = 5 0 11 (4 digit)
(i) 5-digit -5 digit 7 = 645 3 (5 digit)
to give a 3 digit = 76 145 (5 digit)
difference = 308 (3 digit)
(j) 5-digit -5 digit Not possible to give 91,500
Question 2.
Always, Sometimes, Never?
Below are some statements. Think, explore, and find out if each of the statements is ‘Always true’, ‘Only sometimes true’, or ‘Never true’. Why do you think so? Write your reasoning; discuss this with the class.
(a) 5-digit number + 5-digit number gives a 5-digit number
(b) 4-digit number + 2-digit number gives a 4-digit number
(c) 4-digit number + 2-digit number gives a 6-digit number
(d) 5-digit number – 5-digit number gives a 5-digit number
(e) 5-digit number – 2-digit number gives a 3-digit number
Solution:
(a) 5-digit number + 5-digit number gives a 5-digit number: Only sometimes true.
Explanation: Adding two 5-digit numbers can give a number with 5 or 6 digits.
For example, 50.0 + 50,000 = 100,000 (6-digit number), but 20.0 + 30,000 = 50,000 (5-digit number).
(b) 4-digit number + 2-digit number gives a 4-digit number: Only sometimes true.
Explanation: Adding a 2-digit number to a 4-digit number can result in a 4-digit or a 5-digit number.
For example, 1,000 + 99 = 1,099 (4-digit number), but 9,999 + 50 = 10,049 (5-digit number).
(c) 4-digit number + 2-digit number gives a 6-digit number: Never true
Explanation: Adding a 4-digit number to a 2-digit number will always result in a 4-digit or a 5-digit number, never a 6-digit number.
For example, 9,999 + 99 = 10,098 (5-digit number), but it will never reach 6 digits.
(d) 5-digit number – A 5-digit number gives a 5-digit number: Only sometimes true.
Explanation: Subtracting one 5-digit number from another 5-digit number can result in a number with up to 5 digits or fewer.
For example, 50,000 – 10,000 = 40,000 (5-digit number), but 50,000 – 48,000 = 2,000 (4-digit number) or 50,000 – 49,999 = 1 (1-digit number)
(e) 5-digit number – 2-digit number gives a 3-digit number: Never true
Explanation: Subtracting a 2-digit number from a 5-digit number will result in a number with 4 digits.
For example, 10,000 – 99 = 9,901 (4-digit number)
InText Questions (Pages 67-68)
Question 1.
Share and discuss in class the different methods each of you used to solve these questions.
Solution:
Sum of numbers = 12 × 40 + 10 × 50 = 480 + 500 = 980
Solution:
Sum of numbers = 44 × 1 + 20 × 5 = 144

Solution:
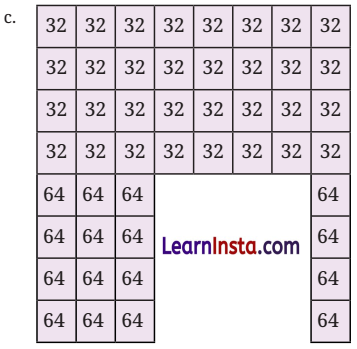
Sum of numbers = 32 × 32 + 16 × 64 = 1024 + 1024 = 2048
Solution:
Sum of numbers = 17 × 3 + 18 × 4 = 51 + 72 = 123
Solution:
Sum of numbers = 15 × 22 + 25 × 22 + 35 × 22 = 330 + 550 + 770= 1650
Solution:
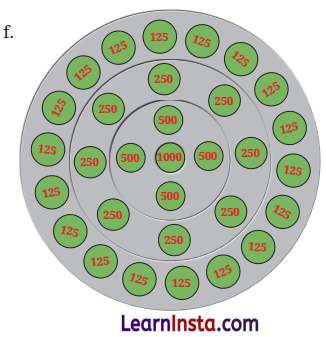
Sum of numbers = 18 × 125 + 8 × 250 + 4 × 500 + 1000 = 2250 + 2000 + 2000 + 1000 = 7250
InText Questions (Page 69)
Question 1.
Make some more Collatz sequences like those above, starting with your favourite whole numbers. Do you always reach 1?
Solution:
Collatz sequence starting with whole number 15 is as follows:
15,46,23,70,35,106,53,160,80, 40,20,10,5,16,8,4,2,1.
Collatz sequence starting with whole number 7 is as follows:
7,22,11,34,17,52,26,13,40,20,10,5,16,8,4,2,1.

3.9 Playing with Number Patterns Figure Out(Pages.no 69 – 70)
We shall do some simple estimates. It is a fun exercise, and you may find it amusing to know the various numbers around us. Remember, we are not interested in the exact numbers for the following questions. Share your methods of estimation with the class.
Question 1.
Steps you would take to walk
(a) From the place you are sitting to the classroom door
(b) Across the school ground from start to end
(c) From your classroom door to the school gate
(d) From your school to your home
Solution:
Do yourself.
(a) 35 steps
(b) 600 steps
(c) 400 steps
(d) 10000 steps
Question 2.
Number of times you blink your eyes or number of breaths you take:
(a) In a minute
(b) In an hour
(c) In a day
Solution:
Number of Times You Blink or Breathe:
(a) In a minute
- Blinking: Count how many times you blink in 10 seconds and multiply by 6.
- Breathing: Count how many times you breathe in 10 seconds and multiply by 6.
(b) In an hour
- Blinking: Multiply the number of blinks per minute by 60.
- Breathing: Multiply the number of breaths per minute by 60.
(c) In a day
- Blinking: Multiply the number of blinks per hour by 24.
- Breathing: Multiply the number of breaths per hour by 24.
Question 3.
Name some objects around you that are:
(a) a few thousand in number
(b) more than ten thousand in number
Solution:
Number of Objects Around You:
(a) A few thousand in number
Examples: Books in a library, grains of rice in a small bag, or items on a large store shelf.
(b) More than ten thousand in number
Examples: Students in a large school district, grains of sand on a small beach, or stars visible in the sky on a clear night.
3.10 An Unsolved Mystery – the Collatz Conjecture! 3.11 Simple Estimation 3.12 Games and Winning Strategies Figure it Out (Page No. 72 – 73)
Question 1.
There is only one supercell (number greater than all its neighbours) in this grid. If you exchange two digits of one of the numbers, there will be 4 supercells. Figure out which digits to swap.
Solution:
If we swap first and last digit of central number 62,871, we get desired result.
| 16,200 | 39,344 | 29,765 |
| 23,609 | 21,876 | 45,306 |
| 19,381 | 50,319 | 38,408 |
Question 2.
How many rounds does your year of birth take to reacall the Kaprekar constant?
Solution:
If your year of birth is 2000
Step 1: Now from digits of number 2000
Here largest number = 2000
and smallest number = 0002
Let’s subtract them = 2000 – 0002 = 1998
Step 2: Now from digits of number 1998
Here largest number = 9981
and smallest number = 1899
Let’s subtract them = 9981 – 1899 = 8082
Step 3: Now from digits of number 8082
Here largest number = 8820
and smallest number = 0288
Let’s subtract them = 8820 – 0288 = 8532
Step 4: Now from digits of number 8532
Here largest number = 8532
and smallest number = 2358
Let’s subtract them = 8532 – 2358 = 6174
which is a Kaprekar constant.
Hence it took 4 rounds to reach the Kaprekar constant from 2000.
Question 3.
We are the group of 5-digit numbers between 35,000 and 75,000 such that all of our digits are odd. Who is the largest number in our group? Who is the smallest number in our group? Who among us is the closest to 50,000?
Solution:
5-digit numbers between 35,000 and 75,000 such that all of our digits are odd are as follows:
35,111, 35,113; 35,115; 35,117; 35,119; …; 39,999; 51,111; 51,113; …; 73,999.
So, the largest number of the group = 73,999
and, the smallest number of the group = 35,111
∴ The number closest to 50,000 = 51,111
Question 4.
Estimate the number of holidays you get in a year including weekends, festivals, and vacations. Then try to get an exact number and see how close your estimate is.
Solution:
To estimate the number of holidays you get in a year, including weekends, festivals, and vacations, follow these steps:
1. Estimate the Number of Holidays:
(a) Weekends:
- There are 52 weeks in a year.
- Each week has 2 weekend days (Saturday and Sunday).
- Estimated Weekends: 52 weeks × 2 days = 104 days
(b) Festivals and Public Holidays:
- This can vary by country and region, but a typical estimate might include around 10-15 public holidays and festivals throughout the year.
(c) School Vacations:
- Depending on your school, there could be around 2-3 weeks of vacation. Assuming 5 working days per week, this amounts to approximately 10-15 additional days.
Total Estimated Holidays:
- Weekends: 104 days
- Festivals and Public Holidays: 10-15 days
- Vacations: 10-15 days
- Total Estimate: 104 + 10 + 10 = 124 days to 104 + 15 + 15 = 134 days
2. Get the Exact Number:
(a) Count Weekends:
Calculate 52 weekends × 2 days = 104 days (this is generally accurate).
(b) Count Public Holidays and Festivals:
Check a calendar for your country or region for an exact count.
(c) Count Vacation Days:
Verify the exact number of vacation days provided by your school or workplace.
Example Calculation:
- Weekends: 104 days
- Public Holidays: 12 days (for example)
- Vacations: 12 days
- Exact Total: 104 + 12 + 12 = 128 days
Comparison:
- Estimated Total: 124 to 134 days
- Exact Total: 128 days
Your estimate of around 124 to 134 days is quite close to the exact number of 128 days, demonstrating that your estimation method was effective.
Question 5.
Estimate the number of liters a mug, a bucket, and an overhead tank can hold.
Solution:
(a) A typical mug holds about 250 to 350 milliliters (0.25 to 0.35 liters).
(b) A common household bucket can hold about 10 to 15 liters.
(c) Overhead tanks come in various sizes, but commonly they hold about 500 to 1000 liters.
Question 6.
Write one 5-digit number and two 3-digit numbers such that theif sum is 18,670.
Solution:
Choose a five-digit number: Let’s pick 15,000.
Determine the sum needed from the three-digit numbers:
- Total sum needed = 18,670
- Subtract the five-digit number from the total: 18,670 – 15,000 = 3,670
Choose two three-digit numbers that add up to 3,670:
- For simplicity, pick numbers that are easy to add.
- Let’s choose 1,800 and 1,870.
- Thus, 15,000 + 1,800 + 1,870 = 18,670
Question 7.
Choose a number between 210 and 390. Create a number pattern similar to those shown in Section 3.9 that will sum up to this number.
Solution:
Let us choose number 300
Now, to get 300, different patterns can be made.
Let’s use a base number of 50 and repeat it multiple times i.e. 6 times
Or
Let’s use 30 and 60 and repeat them to achieve a total of 300.
Question 8.
Recall the sequence of powers of 2 from chapter 1, table 1. Why is the Collatz conjecture correct for all the starting numbers in this sequence?
Solution:
Powers of 2 → 2,4, 8,16,
For 2 (even) → 2 divide by 2 = 1
For 4 (even) → 4 divide by 2 = 2 (even)
→ 2 divide by 2 = 1
For 8 (even) → 8 divide by 2 = 4 (even)
→ 4 divide by 2 = 2 (even)
→ 2 divide by 2 = 1
Thus, for starting numbers that are powers of 2, the Collatz conjecture holds true because the sequence of operations simply involves a series of divisions by 2, which eventual leads to 1.

Question 9.
Check if the Collatz Conjecture holds for the starting number 100.
Solution:
- 100 is even, divide by 2 =50
- 50 is even, divide by 2 = 25
- 25 is odd, so multiply by 3 and add 1 → 76
- 76 is even, divide by 2 = 38
- 38 is even, divide by 2 = 19
- 19 is odd, so multiply by 3 and add 1 → 58
- 58 is even, divide by 2 = 29
- 29 is odd, so multiply by 3 and add 1 → 88
- 88 is even, divide by 2 = 44
- 44 is even, divide by 2 = 22
- 22 is even, divide by 2 = 11
- 11 is odd, so multiply by 3 and add 1 → 34
- 34 is even, divide by 2 = 17
- 17 is odd, so multiply by 3 and add 1 → 52
- 52 is even, divide by 2 = 26
- 26 is even, divide by 2 = 13
- 13 is odd, so multiply by 3 and add 1 → 40
- 40 is even, divide by 2 = 20
- 20 is even, divide by 2 = 10
- 10 is even, divide by 2 = 5
- 5 is odd, so multiply by 3 and add 1 → 16
- 16 is even, divide by 2 = 8
- 8 is even, divide by 2 = 4
- 4 is even, divide by 2 = 2
- 2 is even, divide by 2 = 1
Yes, the Collatz conjecture holds for the starting number 100.




![]()
![]()
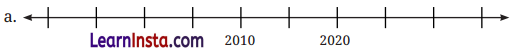

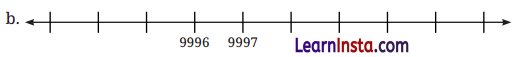






![]()


![]()



![]()






![]()




![]()


![]()

![]()






0 Comments