Lines and Angles Class 6 Solutions | NCERT Ganita Prakriya Chapter 2 Questions and Answers

 

Lines and Angles Class 6 Solutions Questions and Answers

2.1 Point 2.2 Line Segment 2.3 Line 2.4 Ray Figure it Out (Page No. 15-17)

Question 1.

Rihan marked a point on a piece of paper. How many lines can he draw that pass through the point?

Sheetal marked two points on a piece of paper. How many different lines can she draw that pass through both of the points?

Can you help Rihan and Sheetal find their answers?

Solution:

Infinite number of lines can be drawn to pass through a point in a plane.

One and only one line can be drawn to pass through two points.

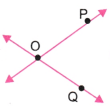
Question 2.

Name the line segments in Fig. 2.4. Which of the five marked points are on exactly one of the line segments? Which are on two of the line segments?

Solution:

Line segments in Fig. 2.4: 

LM

¯¯¯¯¯¯¯¯¯

, 

MP

¯¯¯¯¯¯¯¯¯

, PQ¯¯¯¯¯¯¯¯

 and QR¯¯¯¯¯¯¯¯

Points on exactly one of the line segments: L and R

Points on two of the line segments: M, P, and Q

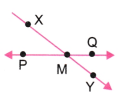
Question 3.

Name the rays shown in given figure. Is T the starting point of each of these rays?

Solution:

Rays in the given figure are 

TA−→−

,

TN−→−

,

TB−→

 and NB−→−

.

Yes, T is the starting point of each of these rays in given figure.

Question 4.

Draw a rough figure and write labels appropriately to illustrate each of the following:

(a) 

OP¯¯¯¯¯¯¯

 and OQ¯¯¯¯¯¯¯¯

 meet at O.

Solution:

(b) 

XY¯¯¯¯¯¯¯¯

 and PQ¯¯¯¯¯¯¯

 intersect at point M.

Solution:

(c) Line l contains points E and F but not point D.

Solution:

(d) Point P lies on AB.

Solution:

Question 5.

In Fig. 2.6, name:

(a) five points

(b) a line

(c) four rays

(d) five-line segment

Solution:

Five points: B, C, O, E and D

A line: 

DB−→−

Four rays: 

OC

−→−

, OB−→−

, OD−→−

 and 

OX

−→−

[Here, one ray has been drawn and the continued point has not been named; thus, we have named it X. Thus, the fourth ray is 

OX

−→−

]

Five line segments: 

DE

−→−

, EO−→−

, BO−→−

, DO−→−

 and CO−→−

Question 6.

Here, a ray 

OA−→−

 in given figure. It starts at 0 and passes through the point A. It also passes through the point B.

(a) Can you also name it as 

OB−→−

? Why?

(b) Can we write 

OB−→−

 as AO−→−

? Why or why not?

Solution:

(a) Yes, we can also name of ray 

OA−→−

 as ray OB−→−

 because initial point of both is same and going on endlessly in the same direction.

(b) No, we cannot not write 

OA−→−

 as AO−→−

 because initial point of a ray cannot be changed.

2.5 Angle Figure it Out (Page No. 19-21)

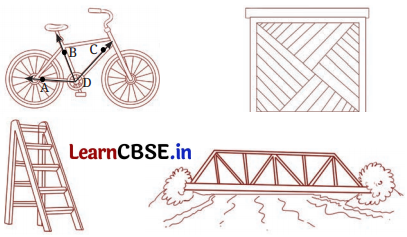
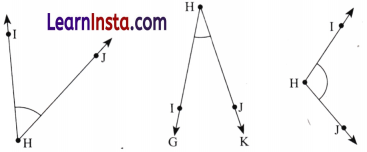
Question 1.

Can you find the angles in the given pictures? Draw the rays forming any one of the angles and name the vertex of the angle.

Solution:

(a) ∠ADB, ∠BDC, vertex: D

(b) ∠PQR, vertex: Q

(c) ∠LMN, vertex: M

(d) ∠XYZ, vertex: Y

Question 2.

Draw and label an angle with arms ST and SR.

Solution:

Question 3.

Explain why ∠APCcannot be labelled as ∠P?

Solution:

In the given figure, PB divides ∠APC in two parts and . makes two angles ∠APB and ∠CPB.

So, ∠APC is greater than ∠APB and ∠CPB.

Therefore, ∠APC cannot be labelled as ∠P.

Question 4.

Name the angles marked in the given figure.

Solution:

The three angles marked in the figure are ∠PTQ, ∠QTR, and ∠PTR.

Question 5.

Mark any three points on your paper that are not on one line. Label them A, B, C. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C? Write them down, and mark each of them with a curve as in Fig. (SeeNCERT Textbook,page 18).

Solution:

We get three lines.

These are line AB, line BC and line CA.

Also, we get three angles.

These are ∠ABC, ∠BCA and ∠CAB.

Question 6.

Now mark any four points on your paper so that no three of them are on one line. Label them A, B, C, and D. Draw all possible lines going through pairs of these points. How many lines do you get? Name them. How many angles can you name using A, B, C, and D? Write them all down and mark each of them with a curve as in Fig. 2.9.

Solution:

Number of lines = 6; 

AB←→

, 

BC

←→

, CD←→

, AD←→

, 

AC

←→

 and BD←→

The number of angles (including A, B, C, and D) = 12; ∠ABC, ∠ABD, ∠DBC, ∠BCD, ∠BCA, ∠ACD, ∠CDA, ∠CDB, ∠BDA, ∠DAB, ∠DAC, and ∠BAC.

2.6 Comparing Angles Figure it Out (Page No. 23)

Question 1.

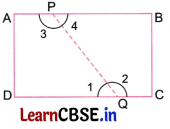
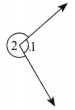
Fold a rectangular sheet of paper, then draw a line along the fold created. Name and compare the angles formed between the fold and the sides of the paper. Make different angles by folding a rectangular sheet of paper and compare the angles. Which is the largest and smallest angle you made?

Solution:

Let’s mark the rectangle and vertex of the fold as shown in figure below.

We get ∠1, ∠2, ∠3 and ∠4.

Comparing: ∠1 < ∠2, ∠4 < ∠3,

∠1 = ∠4, ∠2 = ∠3.

∠2 and ∠3 are the largest angles.

∠1 and ∠4 are the smallest angles.

Question 2.

In each case, determine which angle is greater and why.

(a) ∠AOB or ∠XOY

(b) ∠AOB or ∠XOB

(c) ∠XOB or ∠XOC

Discuss with your friends how you decided which one is greater.

Solution:

(a) ∠AOB > ∠XOY; it is visible that ∠XOY is included within ∠AOB, so ∠AOB > ∠XOY.

(b) ∠AOB > ∠XOB; it is visible that arms OA and OB are open more than arms OX and OB also, ∠XOB is included within ∠AOB.

(c) ∠XOB = ∠XOC; here, the arm OX is common, and the points B and C lie on the same arm thus, ∠XOB = ∠XOC.

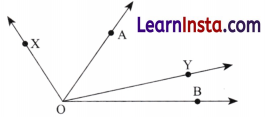
Question 3.

Which angle is greater: ∠XOY or ∠AOB? Give reasons.

Solution:

Here, ∠XOY > ∠AOB.

Using the superimposition method, we can see that ∠XOY > ∠AOB.

Alternatively, it can be seen that the gap between arms OA and OX is greater than the gap between arms OY and OB, thus making the ∠XOY > ∠AOB.

Question 3.

Which angle is greater: ∠XOY or ∠AOB? Give reasons.

Solution:

Using a single letter name like ∠P is insufficient in case of two or more angles having the same vertex. Here, ∠P can be considered for any of the three angles ∠APB, ∠BPC or ∠APC. So, here it is necessary to use three letters in specifying an angle.

2.7 Making Rotating Arms 2.8 Special Types of Angles Figure it Out (Page No. 29-31)

Question 1.

How many right angles do the windows of your classroom contain? Do you see other right angles in your classroom?

Solution:

A window has 4 right angles.

∠1, ∠2, ∠3 and ∠4.

Yes. At comers of door. At comers of blackboard etc.

Question 2.

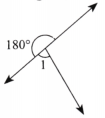
Join A to other grid points in the figure by a straight line to get a straight angle. What are all the different ways of doing it?

Solution:

A straight angle is formed when two points are connected by a straight line, making the angle measure 180°. In simpler terms, it’s a line that continues straight without turning.

To create a straight angle using point A, we need to draw a straight line from A to another grid point in such a way that the line extends in both directions and passes through A.

• Horizontal Line: Connecting A to a grid point directly to the left or right of A.
• Vertical Line: Connecting A to a grid point directly above or below A.
• Diagonal Lines: Connecting A to grid points diagonally (northeast to southwest or northwest to southeast).

Question 3.

Now join A to dther grid points in the figure by a straight line to get a right angle. What are all the different ways of doing it?

Hint: Extend the line further as shown in the figure below. To get a right angle at A, we need to draw a line through it that divides the straight angle CAB into two equal parts.

Solution:

Question 4.

Get a slanting crease on the paper. Now, try to get another crease that is perpendicular to the slanting crease.

(a) How many right angles do you have now? Justify why the angles are exact right angles?

(b) Describe how you folded the paper so that any other person who does not know the process can simply follow your description to get the right angle.

Solution:

(a) You will have four right angles now.

Explanation When you fold the paper to create a crease that is perpendicular to the first, the two creases intersect at a right angle dividing the plane into four right angles of 90° each.

(b) To create a right angle

I. First fold Start by folding the paper so that one corner meets the opposite edge, creating a slant crease.

II. Second fold Now, fold the paper again but this time align the planting crease with the edge of the paper, ensuring the fold is perpendicular to the first crease.

III. Unfold When you open the paper, you will see that the two creases intersect at a 90° angle, forming four right angles.

Explanation The second fold must be made carefully, aligning the first crease with the edge of the paper to insure the two creases are perpendicular. This guarantees that the angles formed are exactly 90°.

2.7 Making Rotating Arms 2.8 Special Types of Angles Figure it Out (Page No. 31-32)

Question 1.

Identify acute, right, obtuse and straight angles in the given figures (See NCERT TB, Page 31).

Solution:

Question 2.

Make a few acute angles and a few obtuse angles. Draw them in different orientations.

Solution:

Question 3.

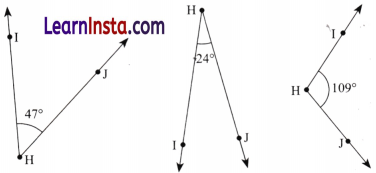
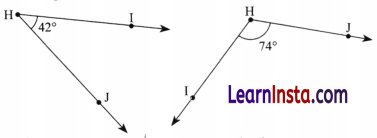
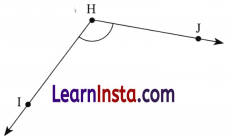
Find the degree measures for the angles given below. Check if your paper protractor can be used here!

Solution:

The student needs to measure the angles on their own using their protractors by keeping the center at H in each case and aligning one arm in such a way that it passes through 0°.

Yes, the paper protractor can be used to measure these angles.

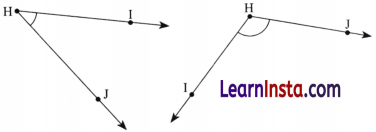
Question 4.

How can you find the degree measure of the angle given below using a protractor?

Solution:

Using a protractor, the angle can be measured in the following way:

We know that the complete angle measure is 360°, and here, the external angle needs to be measured. The interior angle can be measured using the protractor and must be subtracted from 360° to find the exterior angle. Such angles are known as reflex angles.

InText Questions (Page 34)

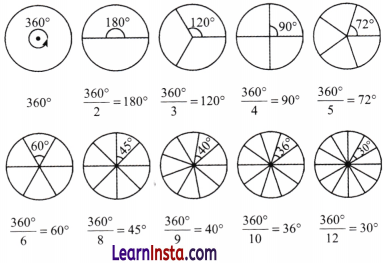
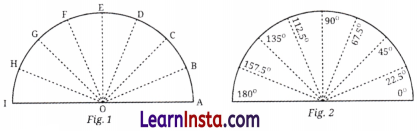
Question 1.

The circle has been divided into 1, 2, 3, 4, 5, 6, 8, 9 10 and 12 parts below. What are the degree measures of the resulting angles? Write the degree measures down near the indicated angles.

Solution:

2.9 Measuring Angles Figure it Out (Page No. 35)

Question 1.

Write the measures of the following angles:

(a) ∠KAL

Notice that the vertex of this angle coincides with the centre of the protractor. So the number of units of 1 degree angle between KA and AL gives the measure of ∠KAL. By counting, we get ∠KAL = 30°.

Making use of the medium sized and large sized marks, is it possible to count the number of units in 5s or 10s?

(b) ∠WAL

(c) ∠TAK

Solution:

(a) ∠KAL = 30°

(b) ∠WAL = 50°

(c) ∠TAK = 120°

InText Questions 

Think! (Pages 39-40)

Question 1.

In given figure, we have ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = ____.

Why?

Solution:

In the given figures 1 and 2, we observe that ∠AOB = ∠BOC = ∠COD = ∠DOE = ∠EOF = ∠FOG = ∠GOH = ∠HOI = 22.5°, because 180° is divided into 8 equal parts, i.e., 

180∘

8

 = 22.5°.

2.9 Measuring Angles Figure it Out (Page No. 40-43)

Question 1.

Find the degree measures of the following angles using your protractor.

Solution:

Question 2.

Find the degree measures of different angles in your classroom using your protractor.

Solution:

Do it yourself.

Question 3.

Find the degree measures for the angles given below. Check if your paper protractor can be used here!

Solution:

The degree measures for the angles shown below.

No, we cannot measures these angles by paper protractor.

Question 4.

How can you find the degree measure of the angle given below using a protractor?

Solution:

We can measure ∠1 = 100° using protractor and subtract it from 360° to find the measure of ∠2 = 260°.

Alternative: We can draw a ray opposite to one of the arms and split the angle into two parts – straight angle and an acute angle. The measure the acute angle (∠1 = 80°) using protractor and add it to 180°. It would be the measure of required angle (180° + 80° = 260°).

Question 5.

Measure and write the degree measures for each of the following angles:

Solution:

(a) 80°

(b) 120°

(c) 60°

(d) 130°

(e) 125°

(f) 62°

Question 6.

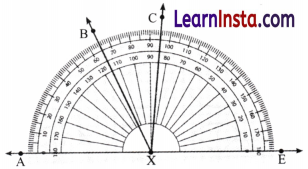
Find the degree measures of ∠BXE, ∠CXE, ∠AXB and ∠BXC.

Solution:

∠BXE = 115°, ∠CXE = 85°, ∠AXB = 65° and ∠BXC = 30°.

Question 7.

Find the degree measures of ∠PQR, ∠PQS and ∠PQT.

Solution:

∠PQR = 45°, ∠PQS = 100° and ∠PQT = 150°.

Question 8.

Make the paper craft as per the given instructions. Then, unfold and open the paper fully. Draw lines on the creases made and measure the angles formed.

Solution:

Do it yourself.

Question 9.

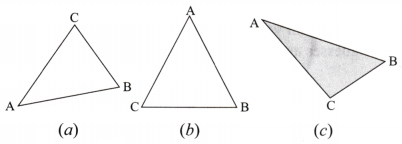
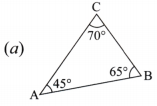
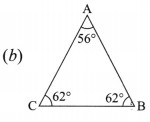
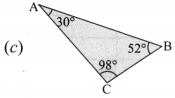
Measure all three angles of the triangle shown in the figure (a) given below and write the measures down near the respective angles. Now add up the three measures. What do you get?

Do the same for the triangles in the figure (b) and (c).

Try it for other triangles as well, and then make a conjecture for what happens in general! We will come back to why this happens in a later year.

Solution:

45°+ 65°+ 70°= 180°

56° + 62°+ 62° = 180°

30° + 52° + 98° = 180°

In general, we observe that sum of all angles of a triangle is 180°.

2.9 Measuring Angles Figure it Out (Page No. 45-46)

Question 1.

Where are the angles?

Angles in a clock:

(a) The hands of a clock make different angles at different times. At 1 o’clock, the angle between the hands is 30°. Why?

(b) What will be the angle at 2 o’clock? And at 4 o’clock? At 6 o’clock?

(c) Explore other angles made by the hands of a clock.

Solution:

(a) A clock has 12 hours, and a full circle is 360°.

Therefore, each hour mark represents 

360∘

12

 = 30°.

(b) The hour hand is at the 2 o’clock position, which is 2 × 30° = 60°

The hour hand is at the 4 o’clock position, which is 4 × 30° = 120°

The hour hand is at the 6 o’clock position, which is 6 × 30° = 180°

(c) At 3 o’ clock, the angle is 3 × 30° = 90°.

At 7:30, the hour hand is halfway between 7 and 8 and the minute hand is at 6, so the angle formed is 45°.

Question 2.

The angle of a door:

Is it possible to express the amount by which a door is opened using an angle? What will be the vertex of the angle, and what will be the arms of the angle?

Solution:

The vertex of the angle in this case is the hinge of the door. This is the point where the door is attached to the door frame and rotates around.

The arms of the angle are the two lines that form the angle:

• One arm is along the door frame (the part that stays fixed).
• The other arm is along the edge of the door that swings open.

The angle represents the degree to which the door is opened. If the door is fully closed, the angle is 0°. If the door is opened, the angle measures how far the door is from being fully closed.

For example:

• If the door is opened to a position where the edge of the door makes a 45° angle with the door frame, then the angle is 45°.
• If the door is opened wider, say to 90°, then the angle is 90°.

Question 3.

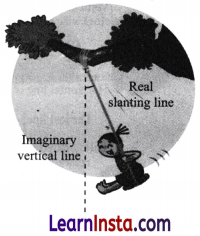
Vidya is enjoying her time on the swing. She notices that the greater the angle with which she starts the swinging, the greater is the speed she achieves on her swing. But where is the angle? Are you able to see any angle?

Solution:

Vidya’s original position is along’the vertical line. When she starts swinging the rope of the swing is along the slanting line which makes an angle with the imaginary vertical line. The speed depends upon this angle.

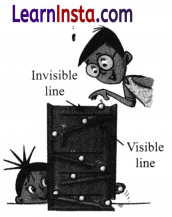
Question 4.

Here is a toy with slanting slabs attached to its sides; the greater the angles or slopes of the slabs, the faster the balls roll. Can angles be used to describe the slopes of the slabs? What are the arms of each angle? Which arm is visible and which is not?

Solution:

Yes, angles can be used to describe the slopes of the slabs. Horizontal imaginary line and slab are the arms of each angle. Here, slab arm is visible but horizontal line is not visible.

Question 5.

Observe the images below where there is an insect and its rotated version. Can angles be used to describe the amount of rotation? How? What will be the arms of the angle and the vertex?

Solution:

Observe the vertical and horizontal lines touching the insects. The rotation from vertical to horizontal position makes an angle. We can imagine the meeting point of the two lines as the vertex, and these two lines as arms of the angle as shown in the picture.

2.10 Drawing Angles Figure it Out (Page No. 49-50)

Question 1.

In Fig. below, list all the angles possible. Did you find them all? Now, guess the measures of all the angles. Then, measure the angles with a protractor. Record all your numbers in a table. See how close your guesses are to the actual measures.

Solution:

The given figure has 20 angles.

Guess: ∠1 = ∠4 = 60°; ∠2 = ∠3 = 120° by actual measure: ∠1 = ∠4 = 70°; ∠2 = ∠3 = 110°.

Question 2.

Use a protractor to draw angles having the following degree measures:

(a)110°

(b) 40°

(c) 75°

(d)1120

(e) 134°

Solution:

Question 3.

Draw an angle whose degree measure is the same as the angle given below:

Also, write down the steps you followed to draw the angle.

Solution:

We can draw an angle equal to the given angle by following these steps:

Step I: Draw a ray 

AB−→−

.

Step II: Measure the angle ZIHJ. It is 118°.

Step III: Place the centre of the protractor at A and the zero edge along 

AB−→−

.

Step IV: Start counting from zero near B. Mark a point C at 118°.

Step V: Join AC.

Thus, ∠BAC = ∠IHJ.

2.11 Types of Angles and their Measures Figure it Out (Page No. 51-52)

Question 1.

In each of the below grids, join A to other grid points in the figure by a straight line to get:

(a) An acute angle

(b) An obtuse angle

(c) A reflex angle

Mark the intended angles with curves to specify the angles. One has been done for you.

Solution:

Question 2.

Use a protractor to find the measure of each angle. Then classify each angle as acute, obtuse, right, or reflex.

a. ∠PTR

b. ∠PTQ

c. ∠PTW

d. ∠WTP

Solution:

(a) ∠PTR = 300 acute

(b) ∠PTQ = 60° acute

(c) ∠PTW = 105° obtuse

(d) ∠WTP = 225° reflex

InText Questions

Let’s Explore (Page 53)

Question 1.

In this figure, ∠TER = 80°.

What is the measure of ∠BET?

What is the measure of ∠SET?

Solution:

Measure of ∠BET = Measure of ∠BER – Measure of ∠TER

= 180° – 80°

= 100°

Measure of ∠SET = Measure of ∠SER – Measure of ∠TER

= 90° – 80°

= 10°

2.11 Types of Angles and their Measures Figure it Out (Page No. 53-54)

Question 1.

Draw angles with the following degree measures:

(a) 140°

(b) 82°

(c) 195°

(d) 70°

(e) 35°

Solution:

(a) 140°

(b) 82°

(c) 195°

(d) 70°

(e) 35°

Question 2.

Estimate the size of each angle and then measure it with a protractor:

Classify these angles as acute, right, obtuse or reflex angles.

Solution:

(a) 45° acute

(b) 150° obtuse

(c) 120° obtuse

(d) 30° acute

(e) 95° obtuse

(f) 350° reflex

Question 3.

Make any figure with three acute angles, one right angle and two obtuse angles.

Solution:

Angles 1, 2 and 3 are acute angles, angle 4 is right angle, angles 5 and 6 are obtuse angles.

Question 4.

Draw the letter ‘M’ such that the angles on the sides are 40° each and the angle in the middle is 60°.

Solution:

Question 5.

Draw the letter ‘Y’ such that the three angles formed are 150°, 60° and 150°.

Solution:

Question 6.

The Ashoka Chakra has 24 spokes. What is the degree measure of the angle between two spokes next to each other? What is the largest acute angle formed between two spokes?

Solution:

The angle between two spokes is 15° (i.e. 360° + 24) because the Ashoka Chakra is a circle and dividing 360° by the number of spokes 24 gives the angle between each pair of adjacent spokes.

The largest acute angle formed between two spokes would be between adjacent spokes, which is 15°.

Question 7.

Puzzle: I am an acute angle. If you double my measure, you get an acute angle. If you triple my measure, you will get an acute angle again. If you quadruple (four times) my measure, you will get an acute angle yet again! But if you multiply my measure by 5, you will get an obtuse angle measure. What are the possibilities for my measure?

Solution:

Let the measure of the angle be m

Then 5 × m > 90 but 4 × m < 90

or m > 

905

 and m < 904

Hence m > 18 but m < 22 ½

Hence measure of the angle is 19° or 20° or 21°