NCERT Class 7 Maths Chapter 8 Working with Fractions Solutions | Question Answer

 

Ganita Prakash Class 7 Chapter 8 Solutions Working with Fractions

NCERT Class 7 Maths Ganita Prakash Chapter 8 Working with Fractions Solutions Question Answer

Figure it Out (Pages 176-177)

Question 1.

Tenzin drinks 

12

 glass of milk every day. How many glasses of milk does he drink in a week? How many glasses of milk did he drink in the month of January?

Solution:

Number of glasses of milk drink in a day = 

12

There are 7 days in a week.

So, number of glasses of milk drink in 1 week = 7 × 

12

 = 72

 = 312

Therefore, Tenzin drinks 3

12

 glasses of milk in a week.

Also, there are 31 days in the month of January.

So, number of glasses of milk drink in the month of January = 31 × 

12

 = 312

 = 1512

Therefore, Tenzin drinks 15

12

 glasses of milk in the month of January.

Question 2.

A team of workers can make 1 km of a water canal in 8 days. So, in one day, the team can make __________ km of the water canal. If they work 5 days a week, they can make __________ km of the water canal in a week.

Solution:

Water canal made by team of workers in 8 days = 1 km

So, water canal made by team of workers in 1 day = 

18

 km

The length of the water canal made by the team of workers in 5 days = 5 × 

18

 km = 58

 km

Hence, the team can make 

58

 km of the water canal in one week.

Question 3.

Manju and two of her neighbours buy 5 litres of oil every week and share it equally among the 3 families. How much oil does each family get in a week? How much oil will one family get in 4 weeks?

Solution:

The amount of oil each family gets in a week = 

53

 litres

The amount of oil one family gets in 4 week = 4 × 

53

 litres = 203

 litres = 623

 litres

Question 4.

Safia saw the Moon setting on Monday at 10 pm. Her mother, who is a scientist, told her that every day the Moon sets 

56

 hours later than the previous day. How many hours after 10 pm will the moon set on Thursday?

Solution:

There are 3 days from Monday to Thursday.

Since the Moon sets 

56

 hours later than previous day,

the number of hours the Moon will set later on Thursday than Monday = 3 × 

56

 hours

= 

156

 hours

= 

52

 hours

We know that 1 hour = 60 minutes

52

 hours = 52

 × 60 minutes = 3002

 minutes = 150 minutes

Now, 150 minutes =120 minutes + 30 minutes = 2 hours 30 minutes

Hence, on Thursday the Moon will set 2 hours 30 minutes after 10 pm.

Question 5.

Multiply and then convert it into a mixed fraction:

(a) 7 × 

35

(b) 4 × 

13

(c) 

97

 × 6

(d) 

1311

 × 6

Solution:

Figure it Out (Pages 180-181)

Question 1.

Find the following products. Use a unit square as a whole for representing the fractions:

(a) 

13

×

15

(b) 

14

×

13

(c) 

15

×

12

(d) 

16

×

15

Solution:

(a) Each row represents 

15

 and each column represents 13

.

The whole is divided into 5 rows and 3 columns, creating 5 × 3 = 15 equal parts and one of the parts

is double-shaded, that is 

115

 of the whole is double-shaded.

Therefore, 

13

×

15

=

115

(b) Each row represents 

13

 and each column represents 14

.

The whole is divided into 3 rows and 4 columns, creating 3 × 4 = 12 equal parts and one of the parts is double-shaded, that is 

12

 of the whole is double-shaded.

Therefore, 

14

×

13

=

112

(c) Each row represents 

12

 and each column represents 15

.

The whole is divided into 2 rows and 5 columns, creating 5 × 2 = 10 equal parts and one of the parts is double-shaded, that is 

110

 of the whole is double-shaded.

Therefore, 

15

×

12

=

110

(d) Each row represents 

15

 and each column represents 16

. The whole is divided into 5 rows and 6 columns, creating 5 × 6 = 30 equal parts and one of the parts is double-shaded, that is 130

 of the whole is double-shaded.

Therefore, 

16

×

15

=

130

Question 2.

Find the following products. Use a unit square as a whole for representing the fractions and carrying out the operations.

(a) 

23

×

45

(b) 

14

×

23

(c) 

35

×

12

(d) 

46

×

35

Solution:

(a) Each row represents 

15

 and each column represents 13

.

The whole is divided into 5 rows and 3 columns creating 5 × 3 = 15 equal parts and 2 × 4 = 8 of the parts are double-shaded, that is 

815

 of the whole is double-shaded.

Therefore, 

23

×

45

=

815

(b) Each row represents 

13

 and each column represents 14

.

The whole is divided into 3 rows and 4 columns, creating 3 × 4 = 12 equal parts and 2 of the parts are double-shaded, that is 

212

 of the whole is double-shaded.

Therefore, 

14

×

23

=

212

 or 16

.

(c) Each row represents 

12

 and each column represents 15

.

The whole is divided into 2 rows and 5 columns, creating 2 × 5 = 10 equal parts and 3 of the parts are double-shaded, that is 

310

 of the whole is double-shaded.

Therefore, 

35

×

12

=

310

(d) Each row represents 

15

 and each column represents 16

.

The whole is divided into 6 × 5 = 30 equal parts, and 4 × 3 = 12 of the parts are double-shaded; that is 

1230

 of the whole is double-shaded.

Therefore, 

46

×

35

=

1230

 or 410

.

Figure it Out (Pages 183-184)

Question 1.

A water tank is filled from a tap. If the tap is open for 1 hour, 

710

 of the tank gets filled. How much of the tank is filled if the tap is open for

(a) 

13

 hour ___________

(c) 

23

 hour ___________

(b) 

34

 hour ___________

(d) 

710

 hour ___________

(e) For the tank to be full, how long should the tap be running?

Solution:

In 1 hour, part of the tank gets filled = 

710

(a) In 

13

 hour, part of the tank gets filled = 13

×

710

 = 730

Therefore, in 

13

 hours, 730

 of the tank gets filled.

(b) In 

23

 hour, part of the tank gets filled = 23

×

710

 = 1430

 = 715

Therefore, in 

23

 hours, 715

 of the tank gets filled.

(c) In 

34

 hours, part of the tank gets filled = 34

×

710

 = 2140

Therefore, in 

34

 hour, 2140

 of the tank gets filled.

(d) In 

710

 hour, part of the tank gets filled = 710

×

710

 = 49100

Therefore, in 

710

 hour, 49100

 of the tank gets filled.

(e) In 1 hour, 

710

 or 7 out of 10 parts of the tank gets filled.

So, in 

17

 × 1 hour, 110

 part of the tank gets filled.

In 

17

 × 10 hours, 1010

 part of the tank gets filled.

So, if the tap is running for 

107

 hours or 137

 hours, the tank will be full.

Question 2.

The government has taken 

16

 of Somu’s land to build a road. What part of the land remains with Somu now? She gives half of the remaining part of the land to her daughter, Krishna, and 13

 it to her son Bora. After giving them their shares, she kept the remaining land for herself.

(a) What part of the original land did Krishna get?

(b) What part of the original land did Bora get?

(c) What part of the original land did Somu keep for herself?

Solution:

After 

16

 part of the land acquiring by government,

The land remaining with Somu is 1 – 

16

 = 56

 parts

(a) Krishna got half of the remaining land.

Since the remaining land is 

56

 of the original land.

So, Krishna get 

12

×

56

 of the original land = 12

×

56

 = 512

Thus, Krishna got 

512

 of the original land.

(b) Bora got 

13

 of the remaining land.

That is 

13

×

56

=

1×53×6

=

518

Thus, Bora got 

518

 of the original land.

(c) Total share of Bora, Krishna, and the government form the original land = 

16

+

512

+

518

=

636

+

1536

+

1036

=

6+15+1036

=

3136

Now, part of land left with Somu = 

1−

3136

=

36−3136

=

536

Thus, Somu kept 

536

 of the original land for herself.

Question 3.

Find the area of a rectangle of sides 3

34

 ft and 935

 ft.

Solution:

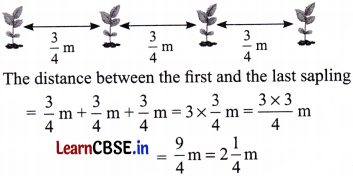
Question 4.

Tsewang plants four saplings in a row in his garden. The distance between two saplings is 

34

 m. Find the distance between the first and last sapling.

[Hint: Draw a rough diagram with four saplings with distance between two saplings as 

34

 m]

Solution:

Question 5.

Which is heavier: 

1215

 of 500 grams or 320

 of 4 kg?

Solution:

Is the Product Always Greater than the Numbers Multiplied?

NCERT In-Text Questions (Page 185)

What can you conclude about the relationship between the numbers multiplied and the product? Fill in the blanks:

• When one of the numbers being multiplied is between 0 and 1, the product is ____________ (greater/less) than the other number.
• When one of the numbers being multiplied is greater than 1, the product is ____________ (greater/less) than the other number.

Solution:

When one of the numbers being multiplied is between 0 and 1, the product is less than the other number.

E.g., 0 < 

12

 < 1, and 12

 × 100 = 50 < 100

When one of the numbers being multiplied is greater than 1, the product is greater than the other number.

E.g., 1

12

 > 1 and 

1

12

×

14

=

32

×

14

=

38

Now, 

14

=

28

⇒ 

14

<

38

8.2 Division of Fractions

Dividend, Divisor, and the Quotient

NCERT In-Text Questions (Pages 189-190)

When do you think the quotient is less than the dividend, and when is it greater than the dividend?

Is there a similar relationship between the divisor and the quotient?

Use your understanding of such relationships in multiplication to answer the questions above.

Solution:

When the divisor is between 0 and 1, the quotient is greater than the dividend.

E.g. 

12

÷

13

=

12

×

31

=

32

=1

12

 and 12

 < 112

When the divisor is greater than 1, the quotient is less than the dividend.

E.g. 

15

÷2=

15

×

12

=

110

 and 110

<

15

.

When the divisor is 1, the quotient is equal to the dividend.

E.g. 

35

÷1=

35

There is no similar relationship between the divisor and the quotient.

8.3 Some Problems Involving Fractions

NCERT In-Text Questions (Page 191)

Example 5.

This problem was posed by Chaturveda Prithudakasvami (c. 860 CE) in his commentary on Brahmagupta’s book Brahmasphutasiddhanta.

Four fountains fill a cistern. The first fountain can fill the cistern in a day. The second can fill it in half a day. The third can fill it in a quarter of a day. The fourth can fill the cistern in one-fifth of a day. If they all flow together, in how much time will they fill the cistern?

Let us solve this problem step by step.

In a day, the number of times-

• The first fountain will fill the cistern in 1 ÷ 1 = 1
• The second fountain will fil the cistern is 1 ÷ 
  12
   = _____
• The third fountain will fil the cistern is 1 ÷ 
  14
   = _____
• The fourth fountain will fil the cistern is 1 ÷ 
  15
   = _____
• The number of times the four fountains together will fill the cistern in a day is ___ + ____ + ___ + ____ = 12.

Solution:

In a day, the number of times-

• The first fountain will fill the cistern in 1 ÷ 1 = 1
• The second fountain will fill the cistern is 1 ÷ 
  12
   = 1 × 21
   = 4
• The third fountain will fill the cistern is 1 ÷ 
  14
   = 1 × 41
   = 4
• The fourth fountain will fill the cistern, is third fountain will fill the cistern is 1 ÷ 
  15
   = 1 × 51
   = 5
• The number of times the four fountains together will fill the cistern in a day is 1 + 2 + 4 + 5 = 12.

Fractional Relations

NCERT In-Text Questions (Page 193)

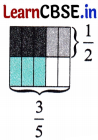
In each of the figures given below, find the fraction of the big square that the shaded region occupies.

Solution:

Consider the following images

We can see in image (i) that the top right square occupies 

14

 of the area of the whole square.

Now, draw similar squares in the other three corners of the whole square as shown in Figure II.

From fig (ii), it is clear that the shaded region is 

(

12

+

12

+

12

)

 of the top right square, that is 32

 of the top right square. But the top right square occupies 14

 of the area of the whole square.

Therefore, the shaded region occupies 

32

×

14

 of the area of the whole square, that is 32

×

14

=

38

 of the area of whole square.

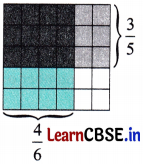
Now, consider the second given images (Fig. IV)

From figure (iii), it is clear that the top left square shown by the bold line occupies 

14

 of the area of the whole square.

Now, from figure (iv) it is clear that the top left square is divided into 8 identical triangles, out of which two are the shaded triangles.

So, the shaded region occupies 

28

 of the top left square. But, the top left square occupies 14

 of the area of the whole.

Therefore the shaded region occupies 

28

×

14

 of the area of the whole square.

That is, 

28

×

14

=

116

Thus, the shaded region occupies 

116

 of the area of the whole square.

A Dramma-tic Donation

NCERT In-Text Questions (Page 194)

If we assume 1 gold dinar = 12 silver drammas, 1 silver dramma = 4 copper panas, 1 copper pana = 6 mashakas, and 1 pana = 30 cowrie shells,

1 copper pana = 

148

 gold dinar 

(

112

×

14

)

1 cowrie shell = ___________ copper panas

1 cowrie shell = ___________ gold dinar.

Solution:

1 copper pana = 

148

 gold dinar 

(

112

×

14

)

1 cowrie shell = 

130

 copper panas

1 cowrie shell = 

148

×

130

 gold dinar = 11440

 gold dinar

Figure it Out (Page 196-198)

Question 1.

Evaluate the following:

Solution:

Question 2.

For each of the questions below, choose the expression that describes the solution. Then simplify it.

(a) Maria bought 8 m of lace to decorate the bags she made for school. She used 

14

 m for each bag and finished the lace. How many bags did she decorate?

(i) 8 × 

14

(ii) 

18

×

14

(iii) 8 ÷ 

14

(iv) 

14

 ÷ 8

(b) 

12

 metre of ribbon is used to make 8 badges. What is the length of the ribbon used for each badge?

(i) 8 × 

12

(ii) 

12

÷

18

(iii) 8 ÷ 

12

(iv) 

12

 ÷ 8

(c) A baker needs 

16

 kg of flour to make one loaf of bread. He has 5 kg of flour. How many loaves of bread can he make?

(i) 5 × 

16

(ii) 

16

 ÷ 5

(iii) 5 ÷ 

16

(iv) 5 × 6

Solution:

(a) To find the total number of bags Maria decorates, we need to divide the total length of lace by the length of the lace required to decorate one bag, i.e., 8 ÷ 

14

.

Hence, the correct expression that describes the solution is (iii) 8 ÷ 

14

Now, 8 ÷ 

14

 = 8 × 4 = 32

(b) To find the length of the ribbon required for one badge, we need to divide the total length of the ribbon by the total number of badges made, i.e., 

12

 ÷ 8.

Hence, the correct expression that describes the solution is (iv) 

12

 ÷ 8.

Now, 

12

÷8=

12

÷

81

=

12

×

18

=

116

(c) To find the total number of loaves of bread that can be made, we need to divide the total weight of flour by the weight of the flour that is required to make the loaf of bread, i.e., 5 ÷ 

16

.

Hence, the correct expression that describes the solution is (iii) 5 ÷ 

16

.

Now, 5 ÷ 

16

 = 5 × 6 = 30

Question 3.

If 

14

 of flour is used to make 12 rotis, how much flour is used to make 6 rotis?

Solution:

If 

14

 kg of flour is required to make 12 rotis, then the amount of flour required to make 6 rotis will be half of 14

 kg,

i.e., 

14

÷2=

14

×

12

=

18

Hence, 

18

 kg of flour is required to make 6 rotis.

Question 4.

Patiganita, a book written by Sridharacharya in the 9th century CE, mentions this problem: “Friend, after thinking, what sum will be obtained by adding together 

1÷

16

,1÷

110

,1÷

113

,1÷

19

, and 1 ÷ 12

”. What should the friend say?

Solution:

Question 5.

Mira is reading a novel that has 400 pages. She read 

15

 of the pages yesterday and 310

 of the pages today. How many more pages does she need to read to finish the novel?

Solution:

15

 of 400 = 15

 × 400 = 4005

 = 80
310

 of 400 = 310

 × 400 = 120

∴ Total number of pages read by Mira = 120 + 80 = 200

Thus, the number of papers she needs to read to finish the novel = 400 – 200 = 200.

Question 6.

A car runs 16 km using 1 litre of petrol. How far will it go using 2

34

 litres of petrol?

Solution:

∴ In 1 litre of petrol, the car runs 16 km.

∴ In 2

34

 litres of petrol, the car will run

Question 7.

Amritpal decides on a destination for his vacation. If he takes a train, it will take him 5

16

 hours to get there. If he takes a plane, it will take him 12

 hour. How many hours does the plane save?

Solution:

The difference between the two durations

Hence, the plane saves 4

23

 hours.

Question 8.

Mariam’s grandmother baked a cake. Mariam and her cousins finished 

45

 of the cake. The remaining cake was shared equally by Mariam’s three friends. How much of the cake did each friend get?

Solution:

The remaining cake is 

1−

45

=

5−45

=

15

So, 

15

 of the cake is shared equally by Mariam’s three friends.

∴ Each of the friend got 

15

÷3=

15

×

13

=

115

∴ Thus, each friend got 

115

 of the cake.

Question 9.

Choose the option(s) describing the product of 

(

565465

×

707676

)

:

(a) > 

565465

(b) < 

565465

 (c) > 707676

(d) < 

707676

 (e) > 1

(f) < 1

Solution:

Hence, the correct options are (a), (c), and (e).

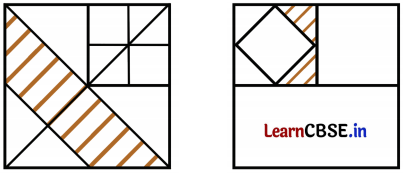
Question 10.

What fraction of the whole square is shaded?

Solution:

In the given figure, the big square is divided into 4 identical squares.

So, one small square occupies 

14

 of the area of the big square.

Now, consider the smaller square

The square in the above figure is divided into 8 identical triangles, of which 3 are the shaded parts.

So, the shaded part is 

38

 of the small square.

But the small square is 

14

 of the big square.

The shaded part is 

14

×

38

=

332

 of the big square.

Hence, 

332

 of the whole square is shaded.

Question 11.

A colony of ants set out in search of food. As they search, they keep splitting equally at each point (as shown in the figure) and reach two food sources, one near a mango tree and another near a sugarcane field. What fraction of the original group reached each food source?

Solution:

At first point ants split into two ways.

So, fraction of ants at each way is 1 ÷ 2 = 

12

At the second point, ants split into two ways.

So fraction of ants at each way = 

12

÷2=

12

×

12

=

14

At the third point, ants split into four ways.

So, fraction of ants at each way = 

14

÷4=

14

×

14

=

116

At the fourth point, ants split into 2 ways.

So fraction of ants at each way = 

116

+2=

116

×

12

=

132

Hence, a fraction of ants at the mango tree is

12

+

14

+

116

+

116

+

132

=

2932

Fraction of ants near sugarcane field is 

132

+

116

=

332

Question 12.

What is 1 – 

12

?

Make a general statement and explain.

Solution:

Here, we observe that in this pattern of product denominator of each term cancels the numerator of the next term, and the final product is the numerator of the first term and the denominator of the last term.

In general, 

(1−

12

)×(1−

13

)×(1−

14

)…×(1−

1n

)=

1n

Puzzle Time (Page 199)

Chess is a popular 2-player strategy game. This game has its origins in India. It is played on an 8 × 8 chequered grid. There are 2 sets of pieces—black and white—one set for each player. Find out how each piece should move and the rules of the game.

Here is a famous chess-based puzzle. From its current position, a Queen piece can move along the horizontal, vertical or diagonal. Place 4 Queens such that no 2 queens attack each other.

For example, the arrangement below is not valid as the queens are in the line of attack of each other.

Solution:

Four queens are placed on this 4 × 4 chequered grid such that no 2 queens attack each other.

Now, place 8 queens on this 8 × 8 grid so that no 2 queens attack each other!

Solution:

8 queens are placed on this 8 × 8 grid so that no 2 queens attack each after.