NCERT Class 7 Maths Chapter 7 A Tale of Three Intersecting Lines Solutions | Question Answer

 

Ganita Prakash Class 7 Chapter 7 Solutions A Tale of Three Intersecting Lines

NCERT Class 7 Maths Ganita Prakash Chapter 7 A Tale of Three Intersecting Lines Solutions Question Answer

NCERT In-Text Questions (Page 146)

What happens when the three vertices lie on a straight line?

Solution:

When the three vertices lie on a straight line, they become collinear. This means they no longer form a triangle because the three points do not enclose any area; they simply align along the same straight path.

7.2 Constructing a Triangle When its Sides are Given

NCERT In-Text Questions (Page 150)

Construct

Construct triangles having the following sidelengths (all the units are in cm):

(a) 4, 4, 6

(b) 3, 4, 5

(c) 1, 5, 5

(d) 4, 6, 8

(e) 3.5, 3.5, 3.5

Solution:

(a) Steps of Construction:

Step 1: Construct the base AB with one of the side lengths.

Let us choose AB = 6 cm.

Step 2: From A, construct a long arc of radius 4 cm.

Step 3: From B, construct an arc of radius 4 cm such that it intersects the first arc.

Step 4: The point where both the arcs meet is the required third vertex C.

Join AC and BC to get ∆ABC.

Note: All the figures drawn in this chapter are proportionally reduced.

(b) Steps of Construction:

Step 1: Construct the base AB with one of the side lengths.

Let us choose AB = 3 cm.

Step 2: From A, construct a sufficiently long arc of radius 4 cm.

Step 3: From B, construct an arc of radius 5 cm such that it intersects the first arc.

Step 4: The point where both the arcs meet is the required third vertex C.

Join AC and BC to get ∆ABC.

(c) Steps of Construction.

Do it yourself.

(d) Steps of Construction.

Do it yourself.

(e) Steps of Construction:

Step 1: Construct the base AB with a side length of 3.5 cm.

Step 2: From A, construct a long arc of radius 3.5 cm.

Step 3: Construct another arc of radius 3.5 cm from B.

Step 4: The point where both the arcs meet is the required third vertex C.

Join AC and BC to get ∆ABC.

Figure it Out (Pages 150-151)

Question 1.

Use the points on the circle and/or the centre to form isosceles triangles.

Solution:

Select any two points on the circle and connect them to the centre of the circle.

Also, join these points to each other. This will form an isosceles triangle as the two radii are equal in length.

Question 2.

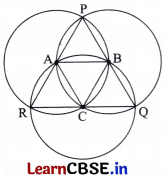
Use the points on the circles and/or their centres to form isosceles and equilateral triangles. The circles are of the same size.

Solution:

An isosceles triangle can be formed by connecting the intersecting points of two circles and the centres of either circle.

Here, isosceles triangles are AXY and BXY.

An equilateral triangle can be formed by connecting the centers of the 2 equal circles and one of their intersecting point.

Here, triangle AXB or triangle AYB is an equilateral triangle.

An equilateral triangle can be formed by connecting the centres of the 3 equal circles.

Here, triangle ABC is an equilateral triangle.

In addition, ∆PAB, ∆QBC, and ∆RAC are also equilateral triangles.

Also, the equilateral triangle is a special case of an isosceles triangle.

So, all these equilateral triangles are also isosceles.

Are Triangles Possible for any Lengths?

NCERT In-Text Questions (Page 151)

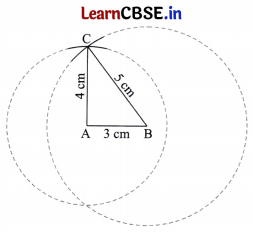
Construct a triangle with sidelengths 3 cm, 4 cm, and 8 cm.

What is happening? Are you able to construct the triangle?

Solution:

Since the arcs from the points A and B do not meet. So, we are not able to construct the triangle with sidelengths 3 cm, 4 cm, and 8 cm.

Here is another set of lengths: 2 cm, 3 cm, and 6 cm. Check if a triangle is possible for these side lengths.

Solution:

The arcs from points A and B do not meet. So, a triangle is not possible for sidelengths 2 cm, 3 cm, and 6 cm.

Triangle Inequality

NCERT In-Text Questions (Page 153)

Can we say anything about the existence of a triangle having sidelengths 3 cm, 3 cm, and 7 cm? Verify your answer by construction.

Solution:

Here, let us choose the direct path length AB = 7 cm.

And, the round about path length = BC + CA = 3 cm + 3 cm = 6 cm.

Since the direct path between two vertices is longer than the roundabout path via the third vertex. So, this triangle is not possible.

Also, by construction existence of a triangle having side lengths 3 cm, 3 cm, and 7 cm is not possible because if we draw arcs from point A and B then they do not meet.

“In the rough diagram given alongside, is it possible to assign lengths in a different order such that the direct paths are always coming out to be shorter than the roundabout paths? If this is possible, then a triangle might exist.”

Solution:

No

Is such a rearrangement of lengths possible in the triangle?

Solution:

No

Figure it Out (Page 154)

Question 1.

We checked by construction that there are no triangles having sidelengths 3 cm, 4 cm, and 8 cm; and 2 cm, 3 cm, and 6 cm. Check if you could have found this without trying to construct the triangle.

Solution:

(a) Consider AB = 4 cm, BC = 3 cm and AC = 8 cm.

Now, direct path length = BC = 3 cm

And, roundabout path length = BA + AC

= 4 cm + 8 cm

= 12 cm

The direct path length is shorter than the roundabout path length.

Also, direct path length = AB = 4 cm

Roundabout path length = AC + BC

= 8 cm + 3 cm

= 11 cm

The direct path length is shorter than the roundabout path length.

Again, direct path length = AC = 8 cm

Then, roundabout path length = AB + BC

= 4 cm + 3 cm

= 7 cm

In this case, the direct path is longer than the roundabout path.

So, a triangle cannot exist.

(b) Consider AB = 3 cm, BC = 2 cm, AC = 6 cm

If we take the direct path = AC = 6 cm.

And, roundabout path length = AB + BC

= 3 cm + 2 cm

= 5 cm

Since the direct path is longer than the roundabout path. So, a triangle cannot exist.

Question 2.

Can we say anything about the existence of a triangle for each of the following sets of lengths?

(a) 10 km, 10 km, and 25 km

(b) 5 mm, 10 m,m and 20 mm

(c) 12 cm, 20 c,m and 40 cm

You would have realised that using a rough figure and comparing the direct path lengths with their corresponding roundabout path lengths is the same as comparing each length with the sum of the other two lengths. There are three such comparisons to be made.

Solution:

(a) When we take the direct path = 25 km.

Then the roundabout path = 10 km + 10 km = 20 km.

Since the direct path is longer than the roundabout path.

So, the existence of a triangle is not possible.

(b) When we take the direct path = 20 mm.

Then the roundabout path = 10 mm + 5 mm = 15 mm.

Since the direct path is longer than the roundabout path.

So, the existence of a triangle is not possible.

(c) When we take the direct path = 40 cm.

Then the roundabout path = 12 cm + 20 cm = 32 cm.

Since the direct path is longer than the roundabout path.

So, the existence of a triangle is not possible.

Question 3.

For each set of lengths seen so far, you might have noticed that in at least two of the comparisons, the direct length was less than the sum of the other two (if not, check again!).

For example, for the set of lengths 10 cm, 15 cm, and 30 cm, there are two comparisons where this happens:

10 < 15 + 30

15 < 10 + 30

But this doesn’t happen for the third length: 30 > 10 + 15.

Solution:

Do it yourself.

NCERT In-Text Questions (Page 154)

Will this always happen? That is, for any set of lengths, will there be at least two comparisons where the direct length is less than the sum of the other two? Explore different sets of lengths.

Solution:

(i) 5 mm, 10 mm, 20 mm.

There are two comparisons where this happens:

10 < 5 + 20 and 5 < 10 + 20 But 20 > 10 + 5

(ii) 12 cm, 20 cm and 40 cm.

There are two comparisons where this happens:

12 < 20 + 40 and 20 <12 + 40 But 40 > 12 + 20

Further, for a given set of lengths, is it possible to identify which lengths will immediately be less than the sum of the other two, without calculations?

[Hint: Consider the direct lengths in the increasing order]

Solution:

Yes, it is possible to identify which lengths will immediately be less than the sum of the other two, if we take the direct lengths in increasing order.

Figure it Out (Page 156)

Question 1.

Which of the following lengths can be the sidelengths of a triangle? Explain your answers. Note that for each set, the three lengths have the same unit of measure.

(a) 2, 2, 5

(b) 3, 4, 6

(c) 2, 4, 8

(d) 5, 5, 8

(e) 10, 20, 25

(f) 10, 20, 35

(g) 24, 26, 28

We observe from the previous problems that whenever there is a set of lengths satisfying the triangle inequality (each length < sum of the other two lengths), there is a triangle with those three lengths as sidelengths.

Solution:

A set of lengths can be the sidelengths of a triangle if each length < the sum of the other two lengths.

(a) 2 < 5 + 2 but 5 > 2 + 2

So, 2, 2, 5 cannot be the sidelengths of a triangle.

(b) 3 < 4 + 6, 4 < 3 + 6, 6 < 4 + 3

So, 3, 4, 6 can be the sidelengths of a triangle.

(c) 2 < 4 + 8, 4 < 2 + 8, but 8 > 4 + 2

So, 2, 4, 8 cannot be the sidelengths of a triangle.

(d) 5 < 5 + 8, 8 < 5 + 5

So, 5, 5, 8 can be the sidelengths of a triangle.

(e) 10 < 20 + 25, 20 < 25 + 10, 25 < 10 + 20

So, 10, 20, 25 can be the sidelengths of a triangle.

(f) 10 < 20 + 35, 20 < 10 + 35, but 35 > 10 + 20

So, 10, 20, 35 cannot be the sidelengths of a triangle.

(g) 24 < 26 + 28, 26 < 24 + 28, 28 < 24 + 26

So, 24, 26, 28 can be the sidelengths of a triangle.

NCERT In-Text Questions (Page 159)

How will the two circles turn out for a set of lengths that do not satisfy the triangle inequality? Find 3 examples of sets of lengths for which the circles:

(а) touch each other at a point,

(b) Do not intersect.

Solution:

When a set of three segment lengths does not satisfy the triangle inequality, it means those segments cannot form a triangle.

However, two circles with these lengths as distances between their centres and points on their circumference can behave differently.

(a) (i) 3, 4, 7 (ii) 5, 2, 3 (iii) 6, 2, 4

(b) (i) 3, 4, 8 (ii) 6, 2, 3 (iii) 5, 1, 2

Figure it Out (Page 159)

Question 1.

Check if a triangle exists for each of the following set of lengths:

(a) 1, 100, 100

(b) 3, 6, 9

(c) 1, 1, 5

(d) 5, 10, 12

Solution:

We know that when each length is smaller than the sum of the other two, we say that the lengths satisfy the triangle inequality, and when a set of lengths satisfies the triangle inequality, then a triangle exists.

(a) Here 1 < 100 + 100, 100 < 100 + 1

So, for sidelengths 1, 100, 100, a triangle exists.

(b) 3 < 6 + 9, 6 < 3 + 9, but 9 = 6 + 3

So, for sidelengths 3, 6, 9, a triangle does not exist.

(c) 1 < 1 + 5, but 5 > 1 + 1

So, for sidelengths 1, 1, 5, a triangle does not exist.

(d) 5 < 10 + 12, 10 < 5 + 12, 12 < 10 + 5

So, for sidelengths 5, 10, and 12, a triangle exists.

Question 2.

Does there exist an equilateral triangle with sides 50, 50, 50? In general, does there exist an equilateral triangle of any sidelength? Justify your answer.

Solution:

Yes, an equilateral triangle with sides 50, 50, 50 exists because the sum of two sides is greater than the third side.

In an equilateral triangle, all sides are equal, so this condition is satisfied.

Yes, an equilateral triangle always exists for any positive sidelength.

For any positive number, say x > 0, an equilateral triangle with all sidelengths x’ exists.

Question 3.

For each of the following, give at least 5 possible values for the third length so there exists a triangle having these as sidelengths (decimal values could also be chosen):

(а) 1, 100

(b) 5, 5

(c) 3, 7

Solution:

(a) 5 possible values for the third length would be 99.5, 99.8, 100, 100.5, 100.9

Since, 100 < 1 + 99.5, 100 < 1 + 99.8, 100 < 1 + 100, 100 < 1 + 100.5, and 100 < 1 + 100.9

(b) 5 possible values for the third length would be 1, 3.5, 5, 7.5, 8.9

Since, 5 < 1 + 5, 5 < 5 + 3.5, 5 < 5 + 5, 5 < 5 + 7.5, and 5 < 5 + 8.9

(c) 5 possible values for the third length would be 4.5, 5, 6.9, 8, 9.8

Since, 7 < 3 + 4.5, 7 < 5 + 3, 7 < 3 + 6.9, 7 < 3 + 8, 7 < 3 + 9.8

NCERT In-Text Questions (Page 160)

See if you can describe all possible lengths of the third side in each case, so that a triangle exists with those side lengths.

For example, in case (a), all numbers strictly between 99 and 101 would be possible.

Solution:

When two sides are given, then the third side must lie between the sum and the difference of the two lengths for the existence of a triangle.

Therefore, (b) numbers will lie between 0 and 10, and (c) numbers will be between 4 and 10.

Figure it Out (Page 161)

Question 1.

Construct triangles for the following measurements, where the angle is included between the sides:

(a) 3 cm, 75°, 7 cm

(b) 6 cm, 25°, 3 cm

(c) 3 cm, 120°, 8 cm

Solution:

(a) Step 1: Construct a side AB of length 7 cm.

Step 2: Construct ∠A = 75° by drawing the other arm of the angle.

Step 3: Mark the point C on the other arm such that AC = 3 cm.

Step 4: Join BC to get the required triangle.

(b) Step 1: Construct a side AB of length 6 cm.

Step 2: Construct ∠A = 25° by drawing the other arm of the angle.

Step 3: Mark the point C on the other arm such that AC = 3 cm.

Step 4: Join BC to get the required triangle.

(c) Step 1: Construct a side AB of length 8 cm.

Step 2: Construct ∠A = 120° by drawing the other arm of the angle.

Step 3: Mark the point C on the other arm such that AC = 3 cm.

Step 4: Join BC to get the required triangle.

Figure it Out (Page 162)

Question 1.

Construct triangles for the following measurements:

(a) 75°, 5 cm, 75°

(b) 25°, 3 cm, 60°

(c) 120°, 6 cm, 30°

Solution:

(a) Step 1: Draw the base AB of length 5 cm.

Step 2: Draw ∠A and ∠B of measure 75° each.

Step 3: The point of intersection of the two new arms of ∠A and ∠B is the third vertex, C.

(b) Step 1: Draw the base AB of length 3 cm.

Step 2: Draw ∠A and ∠B of measure 25°, and 60° respectively.

Step 3: The point of intersection of the two new arms of ∠A and ∠B is the third vertex, C.

(c) Step 1: Draw the base AB of length 6 cm.

Step 2: Draw ∠A and ∠B of measure 30°, and 120° respectively.

Step 3: The point of intersection of the two new arms of ∠A and ∠B is the third vertex, C.

Yes, triangles always exist.

Figure it Out (Page 163)

Question 1.

For each of the following angles, find another angle for which a triangle is (a) possible, (b) not possible. Find at least two different angles for each category:

(a) 30°

(b) 70°

(c) 54°

(d) 144°

Solution:

(a) Another angle for which a triangle is possible will be any angle less than 150°.

Two different angles are 60°, 90°.

Another angle for which a triangle is not possible will be any angle greater than or equal to 150°.

Two different angles are 170°, 160°.

(b) Another angle for which a triangle is possible will be any angle less than 110°.

Two different angles are 70°, 40°.

Another angle for which a triangle is not possible will be any angle greater than or equal to 110°.

Two different angles are 120°, 150°.

(c) Another angle for which a triangle is possible will be any angle less than 126°.

Two different angles are 72°, 54°.

Another angle for which a triangle is not possible will be any angle greater than or equal to 126°.

Two different angles are 140°, 130°.

(d) Another angle for which a triangle is possible will be any angle less than 36°.

Two different angles are 10°, 26°.

Another angle for which a triangle is not possible will be any angle greater than or equal to 36°.

Atleast two different angles are 40°, 50°.

Question 2.

Determine which of the following pairs can be the angles of a triangle and which cannot:

(a) 35°, 150°

(b) 70°, 30°

(c)90°, 85°

(d) 50°, 150°

Solution:

(a) The sum of the given angles = 35° + 150° = 185°.

This is not possible because the total exceeds 180°.

(b) The sum of the given angles = 70° + 30° = 100°.

Possible third angle = 180° – 100° = 80°.

The pairs can be the angles of a triangle.

(c) The sum of the given angles = 90° + 85° = 175°.

Possible third angle = 180° – 175° = 5°.

The pairs can be the angles of a triangle.

(d) The sum of the given angles = 50° + 150° = 200°.

This is not possible because the total exceeds 180°.

NCERT In-Text Questions (Page 164)

What could the measure of the third angle be? Does this measure change if the base length is changed to some other value, say 7 cm? Construct and find out.

Solution:

Given, the measure of two angles is 60° and 70°.

So, the measure of third angle = 180° – 60° – 70° = 50°

No, the measure of the third angle will not change if the base length is changed to some other value, say 7 cm.

Figure it Out (Page 165)

Question 1.

Find the third angle of a triangle (using a parallel line) when two of the angles are:

(a) 36°, 72°

(b) 150°, 15°

(c) 90°, 30°

(d) 75°, 45°

Solution:

(a) Here ∠B = 36° and ∠C = 72°.

Since the line BC is parallel to XY.

So, ∠XAB = ∠B = 36° [Alternate angles] ….. (i)

and ∠YAC = ∠C = 72° [Alternate angles] …… (ii)

Also, ∠XAB + ∠BAC + ∠YAC = 180° [∵∠XAY is a straight angle]

⇒ 36° + ∠BAC + 72° = 180° [Using (i) and (ii)]

⇒ ∠BAC = 180°- 108° = 72°.

(b) Here ∠B = 150° and ∠C = 15°.

Since the line BC is parallel to XY.

So, ∠XAB = ∠B = 150° [Alternate angles] ….. (i)

and ∠YAC = ∠C = 15° [Alternate angles] …… (ii)

Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]

⇒ 150° + ∠BAC + 15° = 180° [Using (i) and (ii)]

⇒ ∠BAC = 180° – 165° = 15°

(c) Here ∠B = 90° and ∠C = 30°.

Since the line BC is parallel to XY.

So, ∠XAB = ∠B = 90° [Alternate angles] …… (i)

and ∠YAC = ∠C = 30° [Alternate angles] …… (ii)

Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]

⇒ 90° + ∠BAC + 30° = 180° [Using (i) and (ii)]

⇒ ∠BAC = 180°- 120° = 60°

(d) Here ∠B = 75° and ∠C = 45°.

Since the line BC is parallel to XY.

So, ∠XAB = ∠B = 75° [Alternate angles] ….. (i)

and ∠YAC = ∠C = 45° [Alternate angles] ….. (ii)

Also, ∠XAB + ∠BAC + ∠YAC = 180° [∠XAY is a straight angle]

⇒ 75° + ∠BAC + 45° = 180° [Using (i) and (ii)]

⇒ ∠BAC = 180° – 120° = 60°

Question 2.

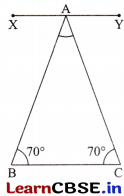
Can you construct a triangle all of whose angles are equal to 70°? If two of the angles are 70°, what would the third angle be? If all the angles in a triangle have to be equal, then what must its measure be? Explore and find out.

Solution:

No, it is not possible to construct a triangle with all angles equal to 70°.

If we take two base angles as 70° that is, ∠B and ∠C = 70°, then we have to find ∠BAC.

Since XY is parallel to BC.

So, ∠XAB = ∠B = 70° ….. (i)

and ∠YAC = ∠C = 70° …… (ii)

Also, ∠XAB + ∠BAC + ∠YAC = 180°

⇒ 70° + ∠BAC + 70° = 180° [Using (i) and (ii)]

⇒ ∠BAC = 180° – 140° = 40°.

So, the third angle would be 40°.

If all the angles in a triangle have to be equal, then each angle must measure 60°. This type of triangle is called an equilateral triangle.

Question 3.

Here is a triangle in which we know ∠B = ∠C and ∠A = 50°. Can you find ∠B and ∠C?

Solution:

Given ∠A = 50° and ∠B = ∠C.

Draw a line XY that is parallel to BC.

Now, ∠XAB = ∠B and ∠YAC = ∠C [Alternate angles] …… (i)

Also, ∠XAB + ∠BAC + ∠YAC = 180°

⇒ ∠B + 50° + ∠C = 180° [Using (i)]

∠B + ∠C = 180° – 50° = 130°

⇒ 2∠B = 130°

⇒ ∠B = 65° = ∠C

Exterior Angles

NCERT In-Text Questions (Page 167)

The angle formed between the extension of a side of a triangle and the other side is called an exterior angle of the triangle. In this figure, ∠ACD is an exterior angle.

Find ∠ACD, if ∠A = 50°, and ∠B = 60°.

From the angle sum property, we know that

50° + 60° + ∠ACB = 180°

110° + ∠ACB = 180°

So, ∠ACB = 70°

So, ∠ACD = 180° - 70° = 110°

Since ∠ACB and ∠ACD together form a straight angle.

Find the exterior angle for different measures of ∠A and ∠B. Do you see any relation between the exterior angle and these two angles?

[Hint: From the angle sum property, we have ∠A + ∠B + ∠ACB = 180°.]

We also have ∠ACD + ∠ACB = 180°, since they form a straight angle.

What does this show?

Solution:

Here, ∠A + ∠B + ∠ACB = 180° ……….(i)

Also, ∠ACD + ∠ACB = 180°

So, ∠ACB = 180° – ∠ACD ……….(ii)

Using (ii) in (i), we get

∠A + ∠B + 180° – ∠ACD = 180°

⇒ ∠A + ∠B = ∠ACD [Exterior angle]

7.4 Constructions Related to Altitudes of Triangles

Altitudes Using Paper Folding

NCERT In-Text Questions (Page 168)

Cut out a paper triangle. Fix one of the sides as the base. Fold it in such a way that the resulting crease is an altitude from the top vertex to the base. Justify why the crease formed should be perpendicular to the base.

Solution:

The perpendicularity happens because the shortest distance between a point, i.e., a vertex, and a line, i.e., the base is always a perpendicular line.

By folding the paper, we construct the shortest distance, ensuring the crease is perpendicular to the base.

7.5 Types of Triangles

NCERT In-Text Questions (Page 170)

What could an acute-angled triangle be? Can we define it as a triangle with one acute angle? Why not?

Solution:

A triangle with all three angles acute is called an acute-angled triangle. We cannot define it with one acute angle because a right/an obtuse triangle also has two acute angles.

Figure it Out (Page 170)

Question 1.

Construct a triangle ABC with BC = 5 cm, AB = 6 cm, CA = 5 cm. Construct an altitude from A to BC.

Solution:

Steps of Construction:

Step 1: Draw the base AB = 6 cm.

Step 2: Using a compass, construct a sufficiently long arc of radius 5 cm from A.

Step 3: Construct another arc of radius 5 cm from B such that it intersects the first arc.

Step 4: The point where both the arcs meet is the required third vertex C. Join AC and BC to get ∆ABC.

Step 5: Keep the ruler aligned to BC. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.

Step 6: Slide the set square along the ruler till the perpendicular edge of the set square touches the vertex A.

Step 7: Draw the altitude through A to BC using the perpendicular edge of the set square.

Question 2.

Construct a triangle TRY with RY = 4 cm, TR = 7 cm, ∠R = 140°. Construct an altitude from T to RY.

Solution:

Steps of Construction:

Step 1: Construct a side TR of length 7 cm.

Step 2: Construct ∠R = 140° by drawing the other arm of the angle.

Step 3: Mark the point Y on the other arm such that RY = 4 cm.

Step 4: Join TY to get the required triangle.

Step 5: Keep the ruler aligned to RY. Place the set square on the ruler such that one of the edges of the right angle touches the ruler.

Step 6: Slide the set square along the ruler till the perpendicular edge of the set square touches the vertex T.

Step 7: Extend the line YR and then draw the altitude through T on YR using the perpendicular edge of the set square.

Question 3.

Construct a right-angled triangle ∆ABC with ∠B = 90°, AC = 5 cm. How many different triangles exist with these measurements?

[Hint: Note that the other measurements can take any values. Take AC as the base. What values can ∠A and ∠C take so that the other angle is 90°?]

Solution:

Given, ∠B = 90°, and AC = 5 cm (hypotenuse)

Since ∠B = 90°,  ∠A and ∠C add upto 90°.

If we fixed AC = 5 cm and ∠A and ∠C vary, then there are infinitely many triangles possible.

Because the shape of the triangle can change with the different values of angles A and C.

One such example is given here:

Question 4.

Through construction, explore if it is possible to construct an equilateral triangle that is (i) right-angled, (ii) obtuse-angled. Also construct an isosceles triangle that is (i) right-angled, (ii) obtuse-angled.

Solution:

An equilateral triangle that is right-angled and obtuse-angled is not possible because each angle of an equilateral triangle is always 60°.

An isosceles right-angled triangle has one angle of 90° and the other two angles of 45° each.

An isosceles obtuse-angled triangle can have one angle as 120° and the other two angles of 30° each.