Ganita Prakash Class 6 Maths Chapter 6 Solutions in Hindi Medium | NCERT Complete Answers

 

Ganita Prakash Class 6 Maths Chapter 6 Solutions in Hindi Medium

आइए पता लगाएँ (पृष्ठ 132)

प्रश्न 1.

लुप्त पदों को ज्ञात कीजिए-

(a) आयत का परिमाप = 14 सेमी; चौड़ाई = 2 सेमी; लंबाई = __________?

(b) वर्ग का परिमाप = एक भुजा की लंबाई 20 सेमी = __________?

(c) आयत का परिमाप = लंबाई 12 मी. = चौड़ाई 3 मी = __________?

हल:

प्रश्न 2.

तार के टुकड़े का प्रयोग करके एक आयत बनाया गया है जिसकी भुजाओं की लंबाइयाँ 5 सेमी और 3 सेमी है। यदि तार को सीधा करके एक वर्ग बनाया जाए, तब वर्ग की एक भुजा की लंबाई क्या होगी?

हल:

तार की लंबाई = आयत का परिमाप

= 2(5 + 3) सेमी

= 16 सेमी

अतः वर्ग की भुजा की लंबाई = 

164

 = 4 सेमी है।

प्रश्न 3.

यदि एक त्रिभुज का परिमाप 55 सेमी है और दो भुजाओं की लंबाइयाँ क्रमशः 20 सेमी और 14 सेमी हैं, तो तीसरी भुजा की लंबाई ज्ञात कीजिए।

हल:

तीसरी भुजा की लंबाई = परिमाप – त्रिभुज की दो भुजाओं की लंबाइयों का योग

= 55 सेमी – (20 + 14) सेमी

= (55 – 34) सेमी

= 21 सेमी

प्रश्न 4.

एक आयताकार पार्क जिसकी लंबाई 150 मी और चौड़ाई 120 मी है, पार्क के चारों ओर ₹ 40 प्रति मीटर की दर से बाड़ लगाने का व्यय ज्ञात कीजिए।

हल:

आयताकार पार्क का परिमाप = 2(लंबाई + चौड़ाई)

= 2(150 + 120) मी

= 540 मी

अतः, ₹ 40 प्रति मीटर की दर से बाड़ लगाने का व्यय = 540 × ₹ 40 = ₹ 21600 है।

प्रश्न 5.

एक धागे के टुकड़े की लंबाई 36 सेमी है। प्रत्येक भुजा की लंबाई क्या होगी, यदि इस धागे से बनाया जाता है-

(a) एक वर्ग

(b) एक त्रिभुज जिसकी सभी भुजाएँ समान लंबाई की हों, और

(e) एक सम षद्भुज (छः भुजाओं वाली बंद आकृति जिसकी सभी भुजाएँ समान लंबाई की हों)?

हल:

(a) वर्ग के लिए, भुजा की लंबाई = 

364

 = 9 सेमी है।

(b) त्रिभुज के लिए, भुजा की लंबाई = 

363

 = 12 सेमी है।

(c) सम षट्भुज के लिए, भुजा की लंबाई = 

366

 = 6 सेमी है।

प्रश्न 6.

एक किसान के आयताकार भूखंड की लंबाई तथा चौड़ाई क्रमश: 230 मी तथा 160 मी है। वह भूखंड के चारों ओर रस्सी द्वारा तीन पूरे चक्कर की बाड़ बनाना चाहता है। जैसा कि पाठ्यपुस्तक में दिए गए चित्र में दिखाया गया है। किसान के द्वारा प्रयोग की गई रस्सी की कुल लंबाई ज्ञात कीजिए।

हल:

भूखंड का परिमाप = 2(230 + 160) मी. = 780 मी है।

अतः बाड़ के 1 चक्कर के लिए आवश्यक रस्सी की लंबाई = 780 मी है।

इसलिए, बाड़ के 3 चक्करों के लिए आवश्यक रस्सी की लंबाई = 3 × 780 मी = 2340 मी है।

आइए पता लगाएँ (पृष्ठ 133-134)

प्रश्न 1.

अक्षी द्वारा 5 चक्करों में तय की गई कुल दूरी ज्ञात कीजिए।

हल:

अक्षी द्वारा 1 चक्कर में तय की गई दूरी = 220 मी है।

अतः, अक्षी द्वारा 5 चक्करों में तय की गई दूरी = 5 × 220 मी = 1100 मी है।

प्रश्न 2.

तोशी द्वारा 7 चक्करों में तय की गई कुल दूरी ज्ञात कीजिए। अक्षी और तोशी में से किसने अधिक दूरी तय की?

हल:

तोशी द्वारा 1 चक्कर में तय की गई दूरी = 2(60 + 30) मी = 180 मी है।

अतः, तोशी द्वारा 7 चक्करों में तय की गई दूरी = 7 × 180 मी = 1260 मी है।

इस प्रकार, तोशी ने अधिक दूरी तय की है।

प्रश्न 3.

सोचिए और निर्देशानुसार स्थितियों को चिह्नित कीजिए-

(a) अक्षी 250 मी दौड़ने के पश्चात् जहाँ पहुँचेगी, उस बिंदु पर ‘A’ चिह्नित कीजिए।

(b) 500 मी दौड़ने के पश्चात् अक्षी जहाँ पहुँचेगी, उस बिंदु पर ‘B’ चिह्नित कीजिए।

(c) अब, अक्षी 1000 मी दौड़ चुकी है। अब बताइए, उसने अपने पथ पर कितने चक्कर पूरे लगाए? उसकी इस स्थिति के बिंदु पर ‘C’ चिह्नित कीजिए।

(d) 250 मी दौड़ने के पश्चात् तोशी जहाँ पहुँचेगी, उस बिंदु पर ‘X’ चिह्नित कीजिए।

(e) 500 मी दौड़ने के पश्चात् तोशी जहाँ पहुँचेगी, उस बिंदु पर ‘Y’ चिह्नित कीजिए।

(f) अब, तोशी 1000 मी दौड़ चुकी है। उसने अपने “पथ पर कितने चक्कर पूरे किए? उसकी स्थिति के बिंदु पर ‘Z’ चिह्नित कीजिए।

हल:

पृष्ठ 134

गहरी सोच- सामान्यतः दौड़ में सभी धावकों के लिए एक समान अंतिम रेखा होती है। यहाँ दो वर्गाकार दौड़-पथ है, जिसमें भीतरी पथ की प्रत्येक भुजा 100 मी है तथा बाहरी पथ की प्रत्येक भुजा 150 मी है। दोनों धावकों के लिए समापन रेखा को चित्र में झंडों द्वारा दर्शाया गया है, जो पथों की भुजाओं में से एक भुजा के मध्य में हैं।

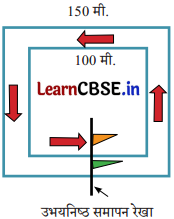
यदि कुल दौड़ 350 मी की है, तो हमें यह पता लगाना होगा कि इन दो पथों पर दोनों धावकों की प्रारंभिक स्थिति कहाँ होनी चाहिए ताकि 350 मी दौड़ने के पश्चात् दोनों की समापन रेखा एक समान हो। भीतरी पथ पर धावक के प्रारंभिक या शुरुआती बिंदु को A के रूप में और बाहरी पथ पर धावक के शुरुआती या प्रारंभिक बिंदु को B के रूप में चिह्नित कीजिए।

हल:

बिंदुओं A और B को प्रश्नानुसार चिह्नित कर दिया गया है। (अगले पृष्ठ पर आकृति देखिए)

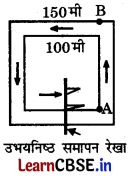
पृष्ठ 134

उभयनिष्ठ समापन रेखा

अक्षी का कहना है कि इस त्रिभुज का परिमाप 9 इकाई है। तोशी का मानना है कि यह 9 इकाई नहीं हो सकती और परिमाप 9 इकाई से अधिक होगा। आप क्या सोचते हैं?

हल:

9 इकाई से अधिक।

पृष्ठ 135

नीचे दी गई आकृतियों का परिमाप सीधी और विकर्ण रेखा इकाइयों का उपयोग करके निकालें।

हल:

पहली आकृति: 8s + 2d है।

दूसरी आकृति: 4s + 6d है।

तीसरी आकृति: 12s + 6d है।

चौथी आकृति: 18s + 6d है।

पृष्ठ 136

अपने आस-पास विभिन्न वस्तुएँ खोजिए जो कि सम आकृतियाँ हों और उनका परिमाप ज्ञात कीजिए। साथ ही अन्य सम बहुभुजों के परिमाप के लिए अपनी समझ को व्यापकीकृत (generalised) रूप दीजिए।

नोट- निर्देशानुसार कीजिए।

पृष्ठ 136

नीचे दी गई अन्य सभी व्यवस्थाओं की सीमा की लंबाई (अर्थात् परिमाप) ज्ञात कीजिए।

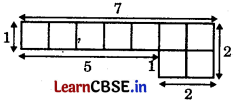
उपर्युक्त चित्रित दोनों टुकड़ों को व्यवस्थित करके एक आकृति बनाइए जिसका परिमाप 22 सेमी हो।

हल:

(b) परिमाप = (2 + 6 + 2 + 6 + 2 + 4 + 6) सेमी = 28 सेमी है।

(c) परिमाप = (6 + 2 + 2 + 6 + 2 + 6 + 2 + 2) सेमी = 28 सेमी है।

(d) परिमाप = (6 + 2 + 3 + 2 + 6 + 2 + 3 + 2) सेमी = 26 सेमी है।

22 सेमी परिमाप के लिए दोनों टुकड़ों को इस प्रकार व्यवस्थित किया जा सकता है:

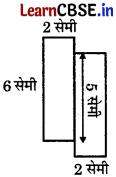
इसका परिमाप = (6 + 2 + 1 + 2 + 6 + 2 + 1 + 2) सेमी = 22 सेमी है।

आइए पता लगाएँ (पृष्ठ 138)

प्रश्न 1.

25 मी लंबे आयताकार बाग का क्षेत्रफल 300 वर्ग मी है। इस बाग की चौड़ाई क्या है?

हल:

बाग की चौड़ाई = 

30025

 मी = 12 मी है।

प्रश्न 2.

8 रुपये प्रति 100 वर्ग मी की दर से 500 मी लंबे और 200 मी चौड़े आयताकार भूखंड पर टाइल लगाने की लागत क्या होगी?

हल:

आयताकार भूखंड का क्षेत्रफल = 500 × 200 वर्ग मी = 100000 वर्ग मी

अतः ₹ 8 प्रति 100 वर्ग मी की दर से टाइल लगाने का व्यय = ₹ 

100000100

 × 8 = ₹ 8000 है।

प्रश्न 3.

एक आयताकार नारियल वाटिका 100 मी लंबी और 50 मी चौड़ी है। यदि प्रत्येक नारियल के पेड़ के लिए 25 वर्ग मी जगह चाहिए, तो इस वाटिका में अधिकतम कितने पेड़ लगाए जा सकते हैं?

हल:

आयताकार नारियल वाटिका का क्षेत्रफल = 100 × 50 वर्ग मी = 5000 वर्ग मी

25 वर्ग मी में, 1 पेड़ लगाया जा सकता है।

अतः 1 वर्ग मी में 

125

 पेड़ लगेंगे।

अतः, 5000 वर्ग मी में लगाए जा सकने वाले पेड़ों की संख्या = 

1×500025

 = 200 है।

प्रश्न 4.

नीचे दी गई आकृतियों को आयताकार भागों में बाँटकर, उनके क्षेत्रफल ज्ञात कीजिए (सभी माप मीटर में दिए गए हैं)।

हल:

पहली आकृति का क्षेत्रफल = (3 × 3 + 7 × 1 + 5 × 2 + 2 × 1 ) वर्ग मी

= (9 + 7 + 10 + 2) वर्ग मी

= 28 वर्ग मी है।

दूसरी आकृति का क्षेत्रफल = (3 × 1 + 3 × 1 + 3 × 1 ) वर्ग मी = 9 वर्ग मी है।

आइए पता लगाएँ (पृष्ठ 139)

आपकी पाठ्यपुस्तक के अंत में दिए गए टैनग्राम के टुकड़े काटिए।

प्रश्न 1.

खोजिए और पता लगाइए कि कितने टुकड़ों का क्षेत्रफल एक समान है।

हल:

टुकड़ों A और B के समान क्षेत्रफल हैं। साथ ही, टुकड़ों C और E के भी समान क्षेत्रफल है।

प्रश्न 2.

आकार D, आकार C की तुलना में कितने गुना बड़ा है? C, D और E में क्या संबंध है?

हल:

आकार D आकार C का दुगुना है, क्योंकि C और E के क्षेत्रफल समान हैं तथा ये दोनों मिलकर आकार D को पूर्णतः ढक लेते हैं। अर्थात् D का क्षेत्रफल = C का क्षेत्रफल + E का क्षेत्रफल है।

प्रश्न 3.

किस आकार का क्षेत्रफल अधिक है- आकार D या आकार F? अपने उत्तर का कारण बताइए।

हल:

उनके क्षेत्रफल बराबर हैं।

प्रश्न 4.

किस आकार का क्षेत्रफल अधिक है- आकार F या G का? अपने उत्तर का कारण बताइए।

हल:

आकार F और G के क्षेत्रफल बराबर हैं।

प्रश्न 5.

आकार G की तुलना में आकार A का क्षेत्रफल कितना है? क्या यह दोगुना बड़ा है? क्या यह चार गुना बड़ा है?

[संकेत : टैनग्राम के टुकड़ों को काटने के पश्चात् एक टुकड़े को दूसरे के ऊपर रखकर हमें ज्ञात होता है कि टुकड़े A और B का क्षेत्रफल एक समान है, टुकड़े C और E का क्षेत्रफल एक समान है। आप इन टुकड़ों से देख सकते हैं कि C और E टुकड़े, D को पूरा ढक लेते हैं। इसका अर्थ है कि D का क्षेत्रफल C और E से दुगुना है।]

हल:

A का क्षेत्रफल G के क्षेत्रफल का दुगुना है।

प्रश्न 6.

क्या अब आप सातों टुकड़ों से बने बड़े वर्ग के क्षेत्रफल को आकार C के क्षेत्रफल के रूप में लिख सकते हैं?

हल:

हाँ। बड़े वर्ग का क्षेत्रफल आकार C के क्षेत्रफल का 16 गुना है।

प्रश्न 7.

इन सातों टुकड़ों को व्यवस्थित करके एक आयत बनाइए। अब इस आयत का क्षेत्रफल, आकार ‘C’ के क्षेत्रफल के रूप में लिखने पर क्या प्राप्त होता है? अपने उत्तर का कारण बताइए।

हल:

अर्थात्, बने आयत का क्षेत्रफल आकार C के क्षेत्रफल का 16 गुना है। इसका कारण यह है कि इन सात टुकड़ों के क्षेत्रफलों में कोई परिवर्तन नहीं होता है।

प्रश्न 8.

क्या इन सातों टुकड़ों से बने वर्ग और आयत के परिमाप भिन्न हैं या समान हैं? अपने उत्तर की व्याख्या कीजिए।

हल:

इन सातों टुकड़ों से बने वर्ग और आयत के परिमाप भिन्न हैं। इसका कारण यह है कि वर्ग और आयत की भुजाओं की लंबाइयाँ भिन्न-भिन्न हैं। वस्तुतः इनसे बने आयत का परिमाप वर्ग के परिमाप से अधिक होगा।

पृष्ठ 140

निम्न आकृतियों का क्षेत्रफल ज्ञात कीजिए-

हल:

पहली आकृति का क्षेत्रफल = 3 + 

12

 + 12

 = 4 वर्ग इकाई।

दूसरी आकृति का क्षेत्रफल = 4 + 2 + 

12

 + 12

 + 12

 + 12

 + 12

 + 12

 = 9 वर्ग इकाई।

तीसरी आकृति का क्षेत्रफल = 7 + 6 × 

12

 = 10 वर्ग इकाई।

चौथी आकृति का क्षेत्रफल = 8 + 6 × 

12

 = 11 वर्ग इकाई।

आइए खोजें! (पृष्ठ 141-142)

एक वर्गाकार ग्रिड पेपर (1 वर्ग = 1 वर्ग इकाई) पर, जितने संभव हो उतने आयत बनाइए जिनकी भुजाएँ पूर्ण संख्याएँ हों तथा जिनका क्षेत्रफल 24 वर्ग इकाई हो।

(a) किस आयत का परिमाप सबसे अधिक है?

(b) किस आयत का परिमाप सबसे कम है?

(c) यदि आप 32 वर्ग सेमी क्षेत्रफल का आयत लेते, तो आपका उत्तर क्या होता? किसी भी क्षेत्रफल को देखते हुए, अधिकतम और न्यूनतम परिमाप वाले आयत के आकार की पहचान बताना संभव है? अपने उत्तर के लिए उदाहरण और कारण दीजिए।

हल:

निर्देशानुसार कीजिए। आयतों की भुजाएँ 24 और 1, 12 और 2, 8 और 3 तथा 6 और 4 इकाइयाँ हो सकती हैं।

(a) भुजाओं 24 और 1 इकाइयों वाले आयत का अधिकतम माप होगा, जो 50 इकाइयाँ हैं।

(b) न्यूनतम परिमाप 20 इकाइयाँ भुजाओं 6 और 4 इकाइयों वाले आयत का होगा।

(c) 32 वर्ग इकाइयों वाले क्षेत्रफल के आयत भुजाओं 32 और 1 इकाइयों, 16 और 2 इकाइयों तथा 8 और 4 इकाइयों के हो सकते हैं। इस स्थिति में, आयत का अधिकतम परिमाप 66 इकाइयाँ और न्यूनतम परिमाप 24 इकाइयाँ होगा। क्षेत्रफल दिया रहने पर अधिकतमं परिमाप वाले आयत के आकार की प्रागुक्ति केवल तभी की जा सकती है, जब भुजाओं की लंबाइयाँ पूर्णांकीय इकाइयों में हों, जैसा कि हमने ऊपर (a) में किया है, अन्यथः हम प्रागुक्ति नहीं कर सकते, क्योंकि परिमाप किसी भी अपरिमित लंबाई का हो सकता है। जहाँ तक न्यूनतम परिमाप वाले आयत की बात है, इसके आकार की प्रागुक्ति की जा सकती है कि यह आयत एक वर्ग होगा।

पृष्ठ 142

प्रश्न 1.

जाँच कीजिए क्या दोनों त्रिभुज एक दूसरे को पूरी तरह आच्छादित (overlap) करते हैं। क्या उनका क्षेत्रफल एक समान है?

हल:

हाँ, हाँ।

प्रश्न 2.

क्या आप इस प्रक्रिया से कुछ निष्कर्ष निकाल सकते हैं? यहाँ लिखिए-

_________________________________

_________________________________

हल:

हाँ, त्रिभुज का क्षेत्रफल = आयत के क्षेत्रफल का 

12

 है।

प्रश्न 3.

क्या तुम नीले आयत एवं पीले त्रिभुज के मध्य और इनके क्षेत्रफल में कुछ संबंध देख सकते हो? यहाँ संबंध लिखिए।

हल:

हाँ, पीले त्रिभुज का क्षेत्रफल = नीले आयत के क्षेत्रफल का 

12

 है।

पृष्ठ 143-144

पिछली कक्षाओं की अपनी समझ का प्रयोग कर ग्रिड पेपर द्वारा किसी भी बंद आकृति के क्षेत्रफल की गणना कीजिए और-

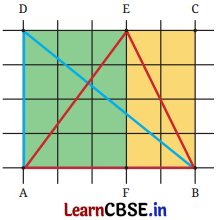
प्रश्न 1.

नीले त्रिभुज BAD का क्षेत्रफल ज्ञात कीजिए।

हल:

10 वर्ग इकाई।

प्रश्न 2.

लाल त्रिभुज ABE का क्षेत्रफल ज्ञात कीजिए।

हल:

10 वर्ग इकाई।

आयत ABCD का क्षेत्रफल = _______________

हल:

20 वर्ग इकाई।

अतः त्रिभुज BAD का क्षेत्रफल, आयत ABCD के क्षेत्रफल का आधा है।

त्रिभुज ABE का क्षेत्रफल = त्रिभुज AEF का क्षेत्रफल त्रिभुज BEE का क्षेत्रफल।

यहाँ, त्रिभुज AEF का क्षेत्रफल = आयत AFED के क्षेत्रफल का आधा।

इसी प्रकार, त्रिभुज BEF का क्षेत्रफल = आयत BFEC के क्षेत्रफल का आधा।

अतः, त्रिभुज ABE का क्षेत्रफल = आयत AFED के क्षेत्रफल का आधा + आयत BFEC के क्षेत्रफल का आधा

= आयत AFED और आयत BFEC के क्षेत्रफलों के योग का आधा

= आयत ABCD के क्षेत्रफल का आधा

निष्कर्ष __________________________________________

_______________________________

हल:

निष्कर्ष:

त्रिभुज का क्षेत्रफल = 

12

 × आधार × ऊँचाई

आइए पता लगाएँ (पृष्ठ 144)

प्रश्न 1.

नीचे दी गई आकृतियों को आयत और त्रिभुजों में विभाजित करके क्षेत्रफल ज्ञात कीजिए:

हल:

आकृतियों (a), (b), (c), (d) और (e) को ऊपर दर्शाए अनुसार विभक्त कीजिए।

आकृति (a) का क्षेत्रफल = (

12

 × 4 × 1 + 5 × 4 + 12

 × 4 × 1) = 24 वर्ग इकाई।

आकृति (b) का क्षेत्रफल = (

12

 × 4 × 3 + 5 × 4 + 12

 × 4 × 2) = 30 वर्ग इकाई।

आकृति (c) का क्षेत्रफल = (

12

 × 6 × 2 + 8 × 3 + 12

 × 3 × 2) + 12

 × 10 × 3) वर्ग इकाई।

= (6 + 24 + 3 + 15)

= 48 वर्ग इकाई।

आकृति (d) का क्षेत्रफल = (

12

 × 2 × 1 + 4 × 3 + 12

 × 2 × 3) = 16 वर्ग इकाई।

आकृति (e) का क्षेत्रफल = (

12

 × 2 × 1 + 12

 × 5 × 1 + 12

 × 2 × 3 + 2 × 2 + 12

 × 2 × 1)

= (1 + 

52

 + 3 + 4 + 1)

= 11

12

 वर्ग इकाई।

पृष्ठ 145

9 इकाई वर्गों का प्रयोग करते हुए निम्नलिखित को हल कीजिए-

प्रश्न 1.

सबसे छोटा संभव परिमाप क्या होगा?

हल:

सबसे छोटा संभव परिमाप 12 इकाई है।

प्रश्न 2.

सबसे बड़ा संभव परिमाप क्या होगा?

हल:

सबसे बड़ा संभव परिमाप 20 इकाई है।

प्रश्न 3.

18 इकाई परिमाप वाली एक आकृति बनाइए।

हल:

18 इकाई परिमाप वाली आकृति नीचे दी गई है:

प्रश्न 4.

क्या आप उपरोक्त तीन परिमापों में से प्रत्येक के लिए अन्य आकार की आकृति बना सकते हैं या क्या उस परिमाप से केवल एक ही आकृति बन सकती है? आपका तर्क क्या होगा?

हल:

हम उपरोक्त तीन परिमापों में से प्रत्येक के लिए, अन्य आकार की आकृतियाँ बना सकते हैं। उदाहरणार्थ, 20 इकाई परिमाप वाले हम निम्नलिखित दो आकार बना सकते हैं:

पृष्ठ 145-146

आइए, कुछ पेचीदा करते हैं, पाठ्यपुस्तक में आकृति दी गई है, जिसका परिमाप 24 इकाई है।

(i) आकृति के पूरे परिमाप की पुनः गणना किए बिना अवलोकन कीजिए, विचार कीजिए और ज्ञात कीजिए कि यदि एक नया वर्ग आकृति में चित्रानुसार जोड़ दिया जाए, तो परिमाप में क्या परिवर्तन होगा?

नए वर्ग को भिन्न-भिन्न स्थानों पर रखिए और सोचिए कि परिमाप में क्या परिवर्तन हो रहे हैं।

(ii) क्या आप इस वर्ग को इस प्रकार रख सकते हैं कि परिमाप में- (a) वृद्धि हो; (b) कमी हो; (c) समान रहे?

हल:

(i) परिमाप में कोई परिवर्तन नहीं होगा। यह वही रहेगा।

(ii) (a) हाँ, (b) हाँ, (c) हाँ।

पृष्ठ 146

पाठ्यपुस्तक में दी गई आकृति में चरण के घर का नक्शा दर्शाया गया है। यह एक आयताकार भूखंड (प्लॉट) है। इस नक्शे को देखिए। आपने क्या अवलोकन किया?

कुछ माप दिए गए हैं:

(a) लुप्त माप की इकाई ज्ञात कीजिए।

(b) उसके घर का क्षेत्रफल ज्ञात कीजिए।

हल:

हम देखते हैं कि घर का नक्शा मीट्रिक इकाइयों में नहीं दिया गया है। साथ ही, कुछ मापन लुप्त हैं।

(a) घर की लंबाई (15 + 5 + 15) = 35 फुट है।

स्टोर रूम का क्षेत्रफल = 3 फुट × 15 फुट = 45 वर्ग फुट है।

छोटा बेडरूम: 15 फुट × 12 फुट,

क्षेत्रफल = 180 वर्ग फुट है।

बगीचा: 3 फुट × (15 + 5) फुट = 3 फुट × 20 फुट,

क्षेत्रफल = 60 वर्ग फुट है।

पार्किंग : फुट × 15 फुट, क्षेत्रफल = 45 वर्ग फुट

हॉल का क्षेत्रफल = (20 × 12 + 5 × 5) वर्ग फुट = 265 वर्ग फुट है।

(b) घर का क्षेत्रफल = 35 फुट × 30 फुट = 1050 वर्ग फुट है।

पृष्ठ 147

कुछ माप दिए गए हैं-

(a) लुप्त माप की इकाई ज्ञात कीजिए।

(b) उसके घर का क्षेत्रफल ज्ञात कीजिए।

शरण के घर में सभी कक्षों की विमाएँ क्या होंगी? शरण और चरण के घरों के क्षेत्रफलों और परिमापों की तुलना कीजिए।

हल:

(a) घर की चौड़ाई (15 + 10) = 25 फुट है।

छोटे बेडरूम का क्षेत्रफल = 120 वर्ग फुट है।

स्टोर रूम का क्षेत्रफल = 10 फुट × 7 फुट = 70 वर्ग फुट है।

प्रसाधन = 5 फुट × 10 फुट = 50 वर्ग फुट है।

हॉल = 23 फुट × 15 फुट = 345 वर्ग फुट है।

प्रवेश = 15 फुट × 7 फुट = 105 वर्ग फुट है।

(b) घर का क्षेत्रफल = 42 फुट × 25 फुट = 1050 वर्ग फुट है।

शरण के घर में, मास्टर बेडरूम के मापन 12 फुट × 15 फुट, छोटे बेडरूम के 12 फुट × 10 फुट तथा हॉल के मापन 23 फुट × 15 फुट हैं।

दोनों घरों के क्षेत्रफल समान अर्थात् 1050 वर्ग फुट हैं।

शरण के घर का परिमाप = 2(42 + 25) फुट

= 2 × 67

= 134 फुट है।

चरण के घर का परिमाप = 2(35 + 30) फुट

= 2 × 65

= 130 फुट है।

इस प्रकार, शरण के घर का परिमाप चरण के घर के परिमाप से 4 फुट अधिक है।

पृष्ठ 148

प्रत्येक (हर) आकृति में लुप्त, एक भुजा की लंबाई या एक क्षेत्र के क्षेत्रफल का मान ज्ञात कीजिए।

हल:

(a) क्षेत्रफल = (13 + 26 – 15) = 24 वर्ग सेमी

(b) क्षेत्रफल = 3 × 3 = 9 वर्ग सेमी

(c) क्षेत्रफल = 4 × 4 = 16 वर्ग सेमी

(d) 18 वर्ग सेमी क्षेत्रफल वाले आयत की चौड़ाई = 

185

 सेमी = 3.6 सेमी है।

अतः, 38 वर्ग सेमी क्षेत्रफल वाले आयत की लंबाई = (4 + 3.6) सेमी = 7.6 सेमी है।

अतः इस आयत की लुप्त चौड़ाई = 18 ÷ 7.6 = 5 सेमी है।

आइए पता लगाएँ (पृष्ठ 149)

प्रश्न 1.

एक आयत की विमाएँ बताइए जिसका क्षेत्रफल उन दो आयतों के क्षेत्रफल के योग के बराबर होगा, जिनकी विमाएँ 5 मी × 10 मी और 2 मी × 7 मी हैं।

हल:

दोनों आयतों के क्षेत्रफलों का योग = 5 मी × 10 मी + 2 मी × 7 मी

= 50 वर्ग मी + 14 वर्ग मी

= 64 वर्ग मी है।

अतः, 64 वर्ग मी क्षेत्रफल वाले एक आयत की विमाएँ’ (पूर्णांकीय लंबाइयों में) 64 मी × 1 मी, 32 मी × 2 मी, 16 मी × 4 मी और 8 मी × 8 मी हो सकती हैं।

प्रश्न 2.

1000 वर्ग मी क्षेत्रफल वाले आयताकार पार्क की लंबाई 50 मी है, पार्क की चौड़ाई ज्ञात कीजिए।

हल:

पार्क की चौड़ाई = 

100050

 मी = 20 मी है।

प्रश्न 3.

एक कमरे के फर्श की लंबाई 5 मी तथा चौड़ाई 4 मी है। 3 मी भुजा वाले एक वर्गाकार कालीन को फर्श पर बिछाया गया है। फर्श के उस भाग का क्षेत्रफल ज्ञात कीजिए जिस पर कालीन नहीं बिछा है।

हल:

फर्श का क्षेत्रफल = 5 × 4 वर्ग मी = 20 वर्ग मी

कालीन का क्षेत्रफल = 3 × 3 वर्ग मी = 9 वर्ग मी

अतः, फर्श के उस भाग का क्षेत्रफल, जिस पर कालीन नहीं बिछा है = (20 – 9) वर्ग मी = 11 वर्ग मी है।

प्रश्न 4.

15 मी लंबे और 12 मी चौड़े एक पार्क के चारों कोनों को खोदकर फूलों की क्यारियाँ बनाई गई हैं, जिनकी लंबाई व चौड़ाई क्रमशः 2 मी और 1 मी है। एक लॉन बनाने के लिए अब कितना क्षेत्रफल उपलब्ध है?

हल:

पार्क का क्षेत्रफल = 15 × 12 वर्ग मी = 180 वर्ग मी

फूलों की 1 क्यारी का क्षेत्रफल = 2 × 1 वर्ग मी = 2 वर्ग मी है।

अतः, फूलों की 4 क्यारियों का क्षेत्रफल = 4 × 2 = 8 वर्ग मी है।

अतः, लॉन के लिए उपलब्ध क्षेत्रफल = (180 – 8) वर्ग मी = 172 वर्ग मी है।

प्रश्न 5.

आकृति A और आकृति B के परिमाप का क्षेत्रफल क्रमशः 18 वर्ग इकाई और 20 वर्ग इकाई है। आकृति A का परिमाप आकृति B के परिमाप से बड़ा है। दी गई स्थिति को पूरा करती हुई दो आकृतियाँ बनाएँ।

हल:

आकृति A:

क्षेत्रफल = 9 × 2 = 18 वर्ग इकाई

इसका परिमाप = 2(9 + 2) इकाई = 22 इकाई

आकृति B:

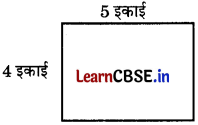
क्षेत्रफल = 5 × 4 = 20 वर्ग इकाई

इसका परिमाप = 2(5 + 4) इकाई = 18 इकाई

यहाँ, आकार A का परिमाप B के परिमाप से अधिक है। (22 > 18)|

प्रश्न 6.

अपनी पुस्तक के एक पृष्ठ पर एक आयताकार हाशिया (border) बनाएँ जो ऊपर और नीचे से 1 सेमी की दूरी पर हो और बाईं व दाईं ओर से 1.5 सेमी दूरी पर हो। हाशिये का परिमाप क्या होगा?

हल:

[नोट: इस प्रश्न की भाषा त्रुटिपूर्ण है। बीच में बनी आकृति को हाशिया नहीं कहना चाहिए। यदि छायांकित भाग को हाशिया लिया जाएगा, तो इसकी दो परिसीमाएँ हैं।]

अछायांकित भाग हाशिया है:

हाशिए ABCD का परिमाप पृष्ठ की लंबाई और चौड़ाई पर निर्भर करेगा।

पृष्ठ की लंबाई और चौड़ाई क्रमश: 30 सेमी और 15 सेमी लेते हुए,

हाशिए का परिमाप = 2(30 – 1.5 – 1.5 + 15 – 1 – 1) सेमी

= 2 × 40 सेमी

= 80 सेंमी है।

प्रश्न 7.

12 इकाई × 8 इकाई आकार का एक आयत बनाइए। इसके अंदर एक अन्य आयत बनाइए जो बाह्य आयत को स्पर्श न करता हो और केवल आधा क्षेत्रफल घेरता हो।

हल:

आयत निर्देशानुसार बना दिए गए हैं:

ABCD का क्षेत्रफल = 96 वर्ग इकाई

EFGH का क्षेत्रफल = 48 वर्ग इकाई = 

12

 ABCD का क्षेत्रफल

प्रश्न 8.

एक वर्गाकार कागज को आधा मोड़ा गया। फिर मोड़ से वर्ग को दो आयतों में काटा गया। वर्ग के आकार को न देखते हुए, निम्न में से एक कथन हमेशा सत्य होगा। यहाँ कौन-सा कथन सत्य है?

(a) प्रत्येक आयत का क्षेत्रफल वर्ग के क्षेत्रफल से बड़ा होगा।

(b) वर्ग का परिमाप, दोनों आयतों के परिमापों के योग से बड़ा होगा।

(c) दोनों आयतों के परिमाप को साथ जोड़ने पर वह हमेशा वर्ग के परिमाप के 1

12

 गुने के बराबर होगा।

(d) वर्ग का क्षेत्रफल हमेशा दोनों आयतों के क्षेत्रफलों को साथ जोड़ने पर प्राप्त क्षेत्रफल से तीन गुना बड़ा होगा।

हल:

केवल कथन (c) सदैव सत्य है।